основание равнобедренной трапеции равны 5 и 15, а ее периметр равен 46. Найдите площадь трапеции
Ответы на вопрос
Ответил ZD96
0
Найдем длину боковых сторон равнобедренной трапеции : (46- 20)/2= 13.
Проведем 2 высоты в трапеции, каждая из которых будет выходить из вершинок тупого угла. Получится прямоугольник. Найдем протиоположенные стороны этого прямоугольника : 5=5.
Тогда найдем оставшиеся отрезки на большей стороне основания этого прямоугльника : (15-5)/2= 5.
Найдем высоту по теореме Пифагора. х^2= 169-25, х= 12
Найдем площадь трапеции S=1/2(основание 1 + основание 2)* высоту = 120
Приложения:
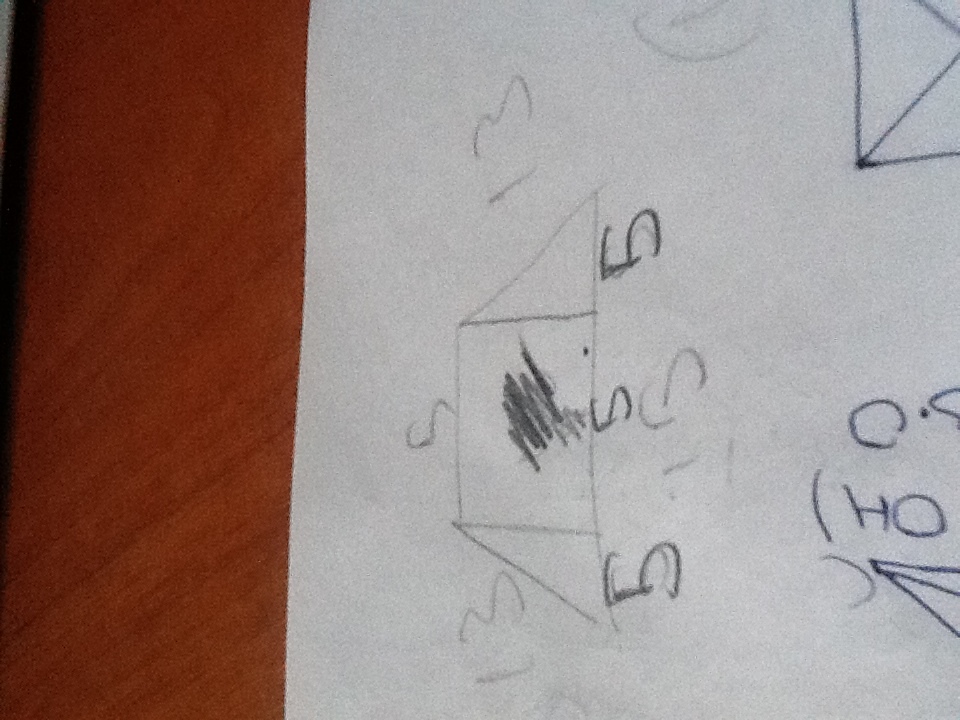
Ответил ElenaChe
0
так как трапеция равнобедренная, следовательно ее боковые стороны равны:
P=a+b+b+c=5+2b+15=46
b=13.
чтобы найти высоту, воспользуемся теоремой Пифагора:
, где
h=12
Приложения:
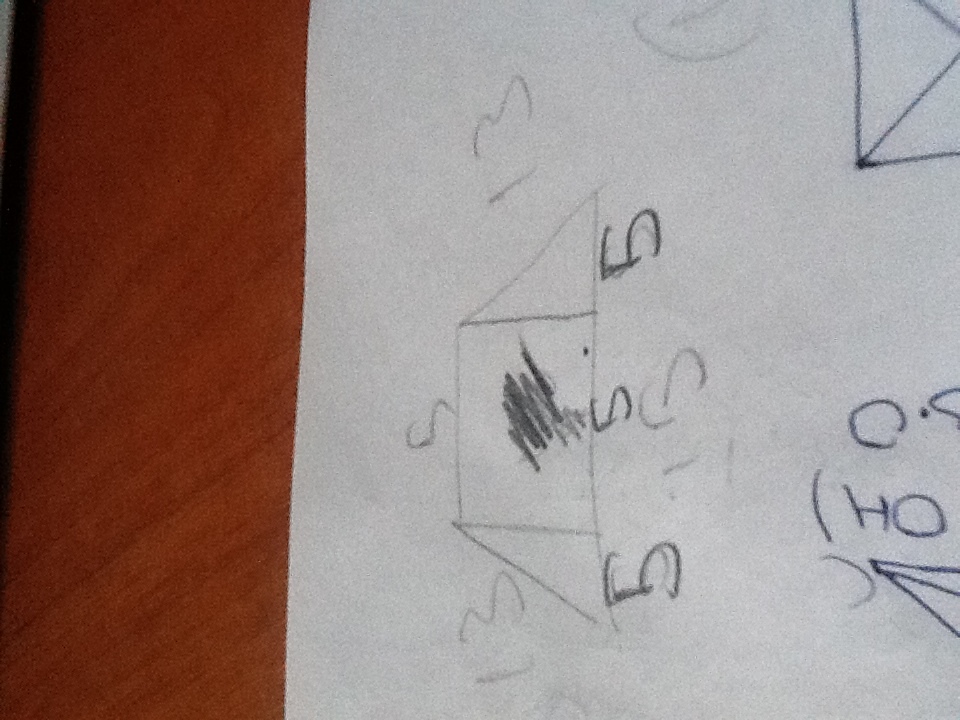
Новые вопросы
Физика,
6 лет назад
Обществознание,
9 лет назад