Основание равнобедренного треугольника равно 4✓2,а медиана ,проведенная к боковой стороне ,равна 5. Найдите длину боковой стороны
Ответы на вопрос
Ответил drama46
7
Ответ:
6
Объяснение:
Квадрат медианы треугольника равен 5² = 25. Пусть х - искомая боковая сторона. Тогда, по формуле длины медианы треугольника, выраженной через 3 его стороны, получаем: 2х² + 2*(4√2)² - х² = 25*4, откуда х = 6
Ответил Аноним
6
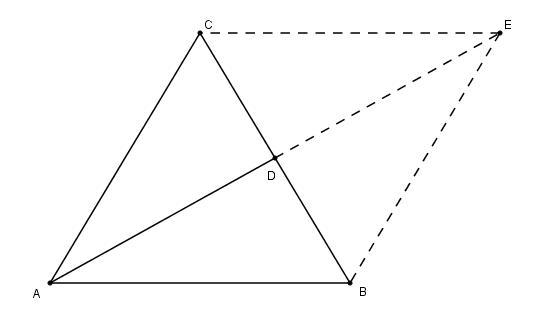
Достроим до параллелограмма ACEB, в нём AE = 2AD = 10
CE = AB = 4√2 и AC = CB = BE.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон
Ответ: 6
Приложения:
Новые вопросы
Английский язык,
1 год назад
Литература,
1 год назад
Математика,
1 год назад
Химия,
1 год назад
География,
6 лет назад