Основание равнобедренного треугольника равно 110, косинус угла при вершине равен 5/13. Две вершины прямоугольника лежат на основании треугольника, а две другие – на боковых сторонах. Найдите площадь прямоугольника, если известно, что одна из его сторон вдвое больше другой.

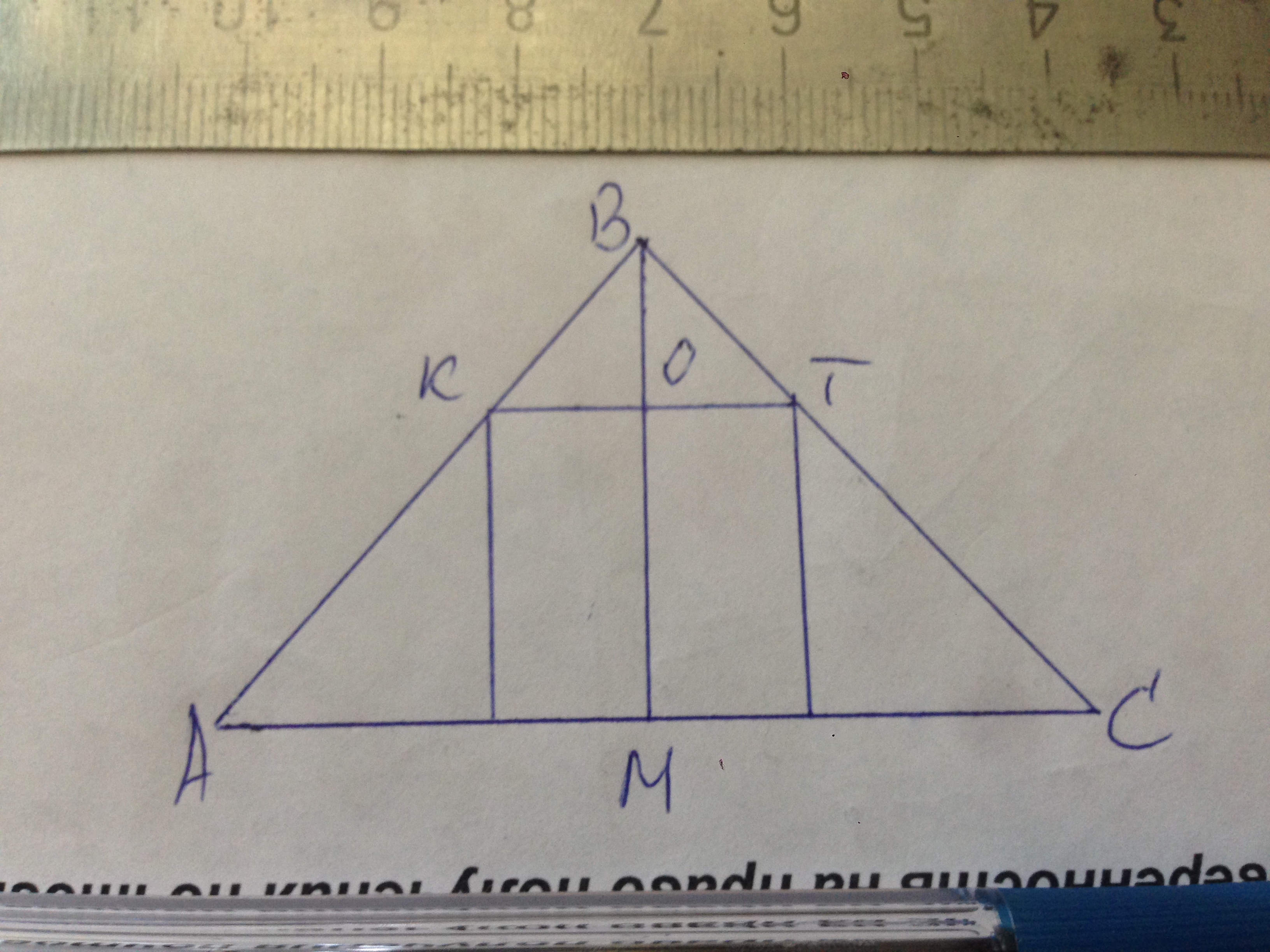
Пусть АВ=ВС=а, АС=b, α - угол при вершине.
В тр-ке АВС по т. косинусов а²=b²+b²-2·b·b·cosα=2b²-2b²·5/13,
16b²/13=110²,
b²=110²·13/16.
В равнобедренном тр-ке высота равна: h=b²/2R=b²/(a/sinα).
sin²α=1-cos²α=1-25/169=144/169,
sinα=12/13.
BM=h=(110²·13/16)/(110·13/12)=110·3/4=82.5
Треугольники АВС и КВТ подобны по трём углам, значит АС/КТ=ВМ/ВО.
1) Пусть КТ=х, ОМ=2х, значит ВО=ВМ-ОМ=82.5-2х.
110/х=82.5/(82.5-2х) ⇒ х=30, 2х=60.
Площадь прямоугольника S=x·2x=30·60=1800 (ед²) - это ответ.
2) пусть ОМ=х, КТ=2х, значит ВО=82.5-х.
110/2х=82.5/(82.5-х) ⇒ х=33, 2х=66.
S=33·66=2178 (ед²) - это ответ.

Есть и второй вариант, когда КТ вдвое больше ОМ, его тоже следует рассмотреть, где стороны прямоугольника равны 30 и 60, а площадь 30*60 = 1800

обратите внимание, я уже рассмотрел оба варианта.

Спасибо, я поторопился.