Осевое сечение конуса есть равнобедренный прямоугольный треугольник с площадью 16см^2.найдите объем конуса

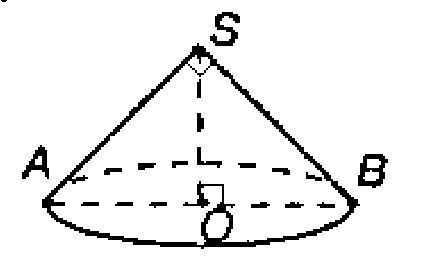
объем конуса равен Vкон.=1/3*ПR^2*h(или глядя на рисунок Vкон.=1/3*OB^2*SO)
в равнобедренном прямоугольном треугольнике (глядя на рисунок) ASB  AS=SB, тогда Sabc=1/2*AS*SB
AS=BS=корень2*S=корень2*16=корень32=4корень2см
тогда AB=корень AS^2+BS^2=корень 32+32=корень 64=8см(это у нас диаметр=> радиус равен 4)
находим OS=AS*sin45(т.к на рисунке видно угол 45 градусов)=4корень2*корень2/3=2.6м
НАХОДИМ Vкон.=1/3П*4^2*2.6=примерно 13.8П
ОТВЕТ 13.8П