Определите количество решений системы графическим методом:
Запишите алгоритм построения заданных графиков и подпишите их при построении.
Приложения:
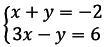
Ответы на вопрос
Ответил kamilmatematik100504
6
Ответ: (1 ; -3 )
Объяснение:
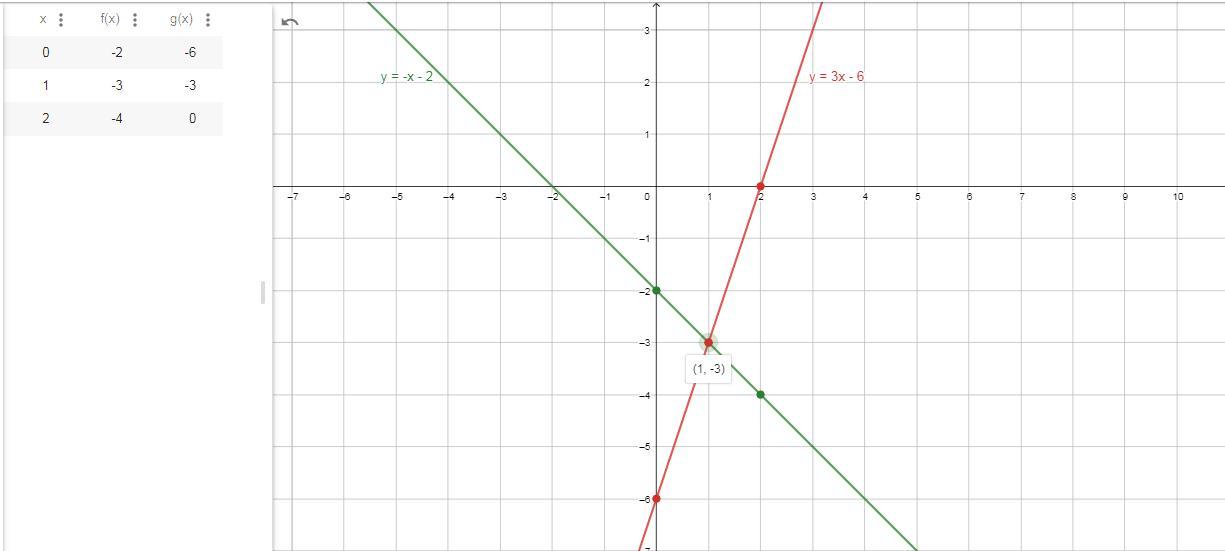
Запишем данные графики в стандартном виде
y = kx+b
Сделаем таблицу значений для каждого графика
1) y = -x-2
2) y = 3x-6
Приравняем их , чтобы найти точку пересечения
Так как у нас график линейной функции он имеет одно решение
(1 ; -3 )
Приложения:
Ответил ludmilaksenija2005
5
Объяснение:
{Х+у= - 2
{3х-у=6
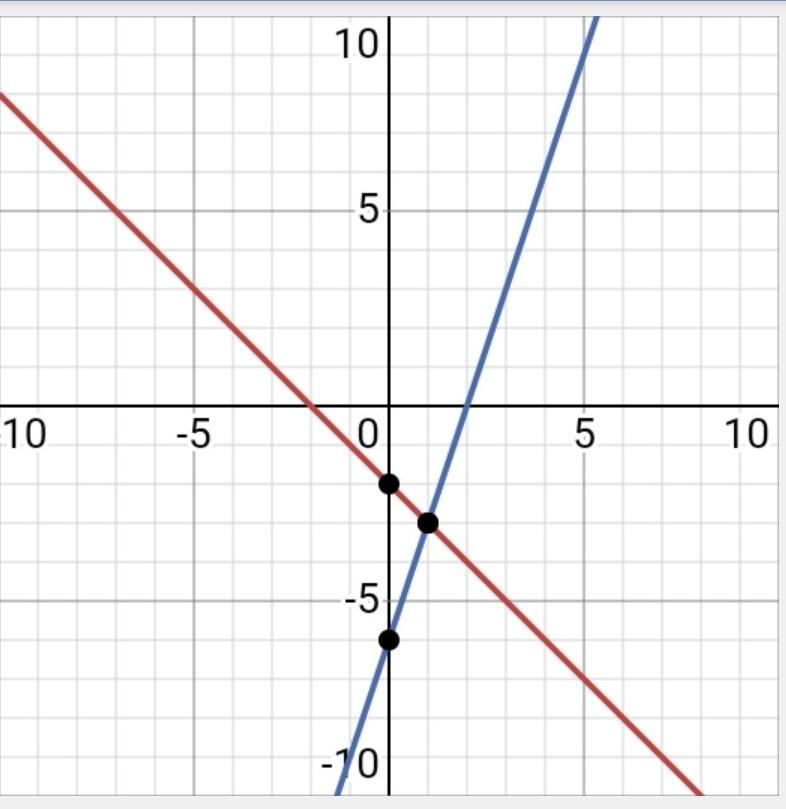
Строим график уравнения
Х+у= - 2 красная прямая
У= - 2-х
Х 0 1
У - 2 - 3
Строим график уравнения
3х-у=6 синяя прямая
-у=6-3х
У=3х-6
Х 1 0
У - 3 - 6
Находим точку пересечения (1; - 3)
Приложения:
nahievdaniar52:
яовттч
fdhdh
Новые вопросы
Русский язык,
1 год назад
Алгебра,
6 лет назад
Физика,
6 лет назад
Математика,
8 лет назад
Литература,
8 лет назад