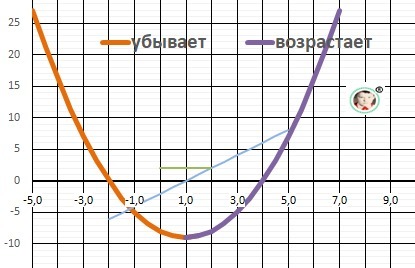
опишите свойства функции у=х²-2х-8 по следующей схеме :1) д (у) =
2)Е (у)
3 нули функции :
4)у>0 при х э, у<0 при хэ
5)у убывает при х э, у возрастает при х э
Ответы на вопрос
ДАНО: Y(x) = x² -2*x -8
ИССЛЕДОВАНИЕ.
1. Область определения D(y) = R, Х∈(-∞;+∞) - непрерывная , гладкая
2. Пересечение с осью OХ.
Решаем квадратное уравнение: D = 36, x1 = -2, x2 = 4
3. Интервалы знакопостоянства.
Y>0 - X∈(-∞;-2]∪[4;+∞)
Y<0 - X∈[-2;4]
4. Пересечение с осью OY. Y(0) = -8
5. Исследование на чётность.
Y(-x) ≠ Y(x) - не чётная. Y(-x) ≠ -Y(x), Функция ни чётная, ни нечётная - функция общего вида.
6. Первая производная. Y'(x) = 2*x -2 = 0
Х = 1 - корень производной.
7. Локальные экстремумы.
Ymin(1) = - 9.
8. Интервалы возрастания и убывания.
Возрастает: X∈[1;+∞)
Убывает: Х∈(-∞;1]
9. Вторая производная - Y"(x) = 2
10. Вогнутая - "ложка" - везде - Х∈R.
11. E(y) = [-8;+∞) - область значений.
12. График в приложении.