Окружности ωb и ωc лежат вне треугольника ABC, касаются внутренним образом описанной около треугольника ABC окружности в точках B1 и C1 соответственно и сторон AC и AB в точках B2 и C2 соответственно. Прямые B1B2 и C1C2 повторно пересекают описанную окружность треугольника в точках B3 и C3 соответственно, причём точки расположены, как показано на картинке. Найдите угол между прямыми CB3 и BC3, если ∠BAC=72∘.
Ответы на вопрос
Ответил siestarjoki
10
Докажем лемму Архимеда.
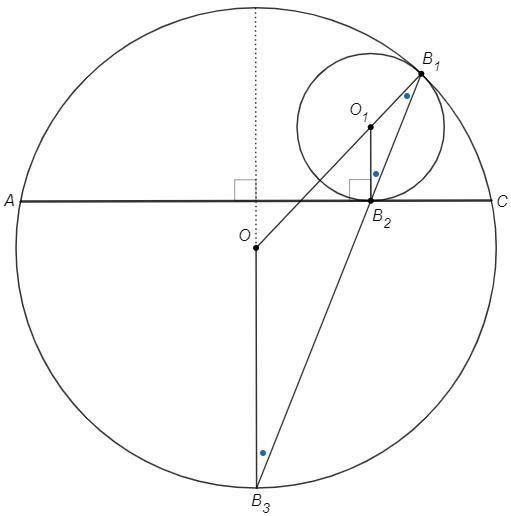
Точка касания B1 лежит на линии центров OO1.
B1O1B2 и B1OB3 - равнобедренные, ∠B1=∠B2=∠B3
O1B2||OB3 (соответственные углы равны)
O1B2⊥AC (радиус перпендикулярен касательной) => OB3⊥AC
Диаметр через B3 перпендикулярен хорде AC, следовательно делит дуги AC и AC' пополам.
B3 - середина дуги AC => диаметр через B3 перпендикулярен хорде AC, ∠M=90.
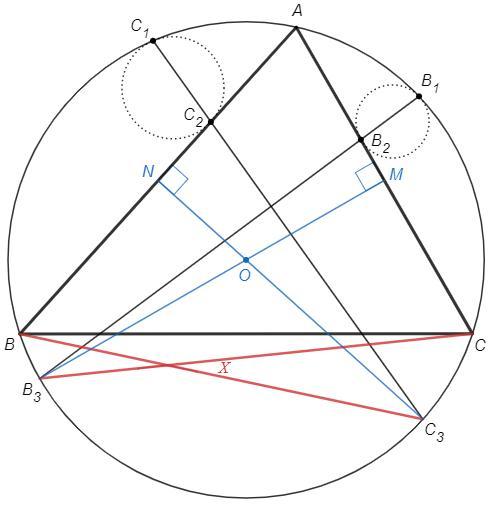
Аналогично ∠N=90
∪B3C3 =∠B3OC3 =∠MON =180-∠A (из четырехугольника AMON)
∪BC =2∠A
∠X =(∪BB3+∪CC3)/2 =(∪BC-∪B3C3)/2 =3/2 ∠A -90 =18° (угол между хордами)
Если прямые CB3 и BC3 пересекаются вне окружности - угол X между секущими.
∠X =(∪CC3-∪BB3)/2 =(∪BC-∪B3C3)/2 =3/2 ∠A -90 =18°
Приложения:

Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Литература,
2 года назад
Математика,
2 года назад