Окружность, проходящая через середины сторон AB, BC и вершину B треугольника ABC, касается стороны AC. Найдите длину стороны AC, если AB=3, BC=5
Ответы на вопрос
Ответил Пеппер
0
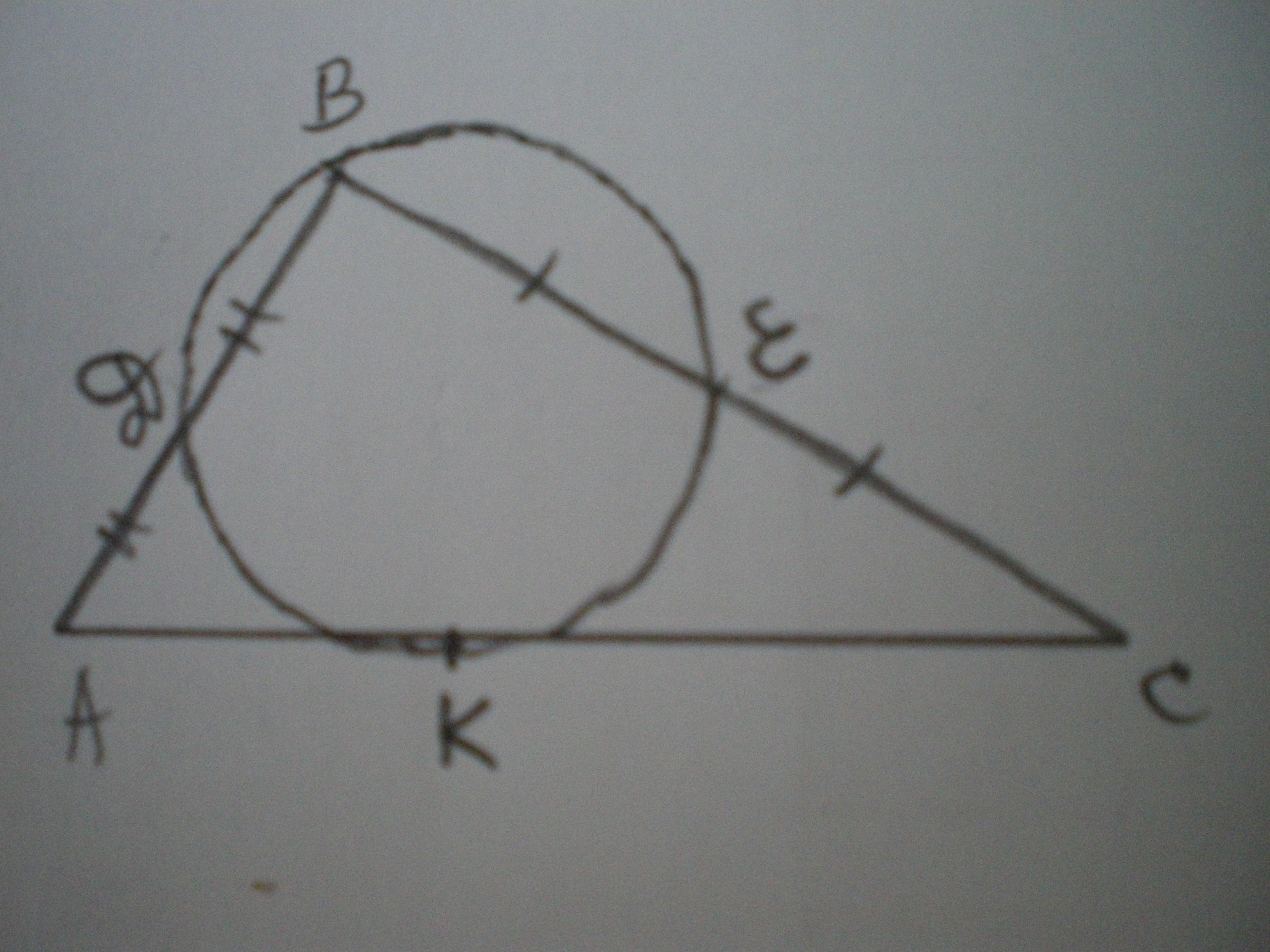
Дано: ΔАВС, АВ=3, ВС=5. АД=ДВ=1,5; ВЕ=ЕС=2,5.
Найти АС.
Воспользуемся теоремой: Для касательной и секущей к окружности, проведённых из одной точки, квадрат расстояния от этой точки до точки касания равен произведению длины секущей на длину её внешней части.
Тогда АК²=АВ*АД=3*1,5=4,5; АК=√4,5≈2,12
КС²=СВ*СЕ=5*2,5=12,5; КС≈3,54;
АС=2,12+3,54=5,66 (ед.изм)
Приложения:
Ответил LFP
0
удобнее было записать: АК²=3*1,5=2*1,5*1,5 и тогда АК = 1.5√2; аналогично КС=2.5√2; и вся АС = 4√2;
Новые вопросы