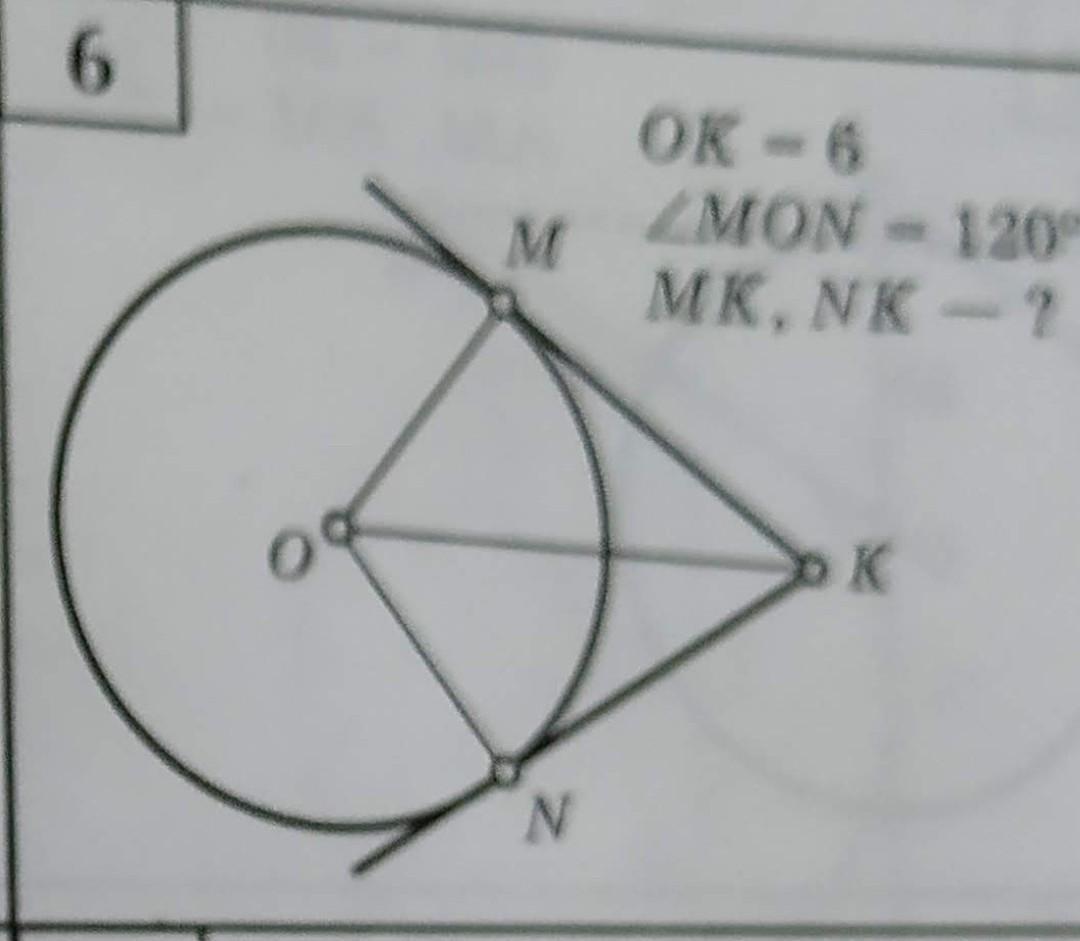
OK = 6
угол MON = 120°
найти стороны MK, NK​

OM = ON как радиусы окружности. Радиус перпендикулярен касательной, проведенный в его точку касания, значит

У прямоугольных треугольников и гипотенуза общая и катеты , значит эти треугольники равны по катету и гипотенузе. У равных треугольников соответствующие элементы (стороны, углы) равны

отсюда следует, что - биссектриса угла , значит

Ответ: MK = NK = 3√3.