Одна из сторон параллелограмма равна 15 , а другая 4√13 , а тангенс одного из углов 2/3. Найти площадь параллелограмма.
Ответы на вопрос
Дано:
ABCD — параллелограмм.
AB = CD = 4√13;
AD = BC = 15;
tg ∠B = .
Найти:
.
Решение:
- Способ №1:
Тангенс угла равен отношению синуса этого угла к косинусу.
Это значит, что синус угла B относится к косинусу угла B как 2 : 3.
Пусть коэффициент пропорциональности равен x, тогда sin∠B = 2x, cos∠B = 3x.
Согласно основному тригонометрическому тождеству:
sin²∠B + cos²∠B = 1
(2x)² + (3x)² = 1
4x² + 9x² = 1
13x² = 1
x² =
x =
.
Найдем площадь параллелограмма, умножив две его стороны на синус угла между ними:
(кв. единиц).
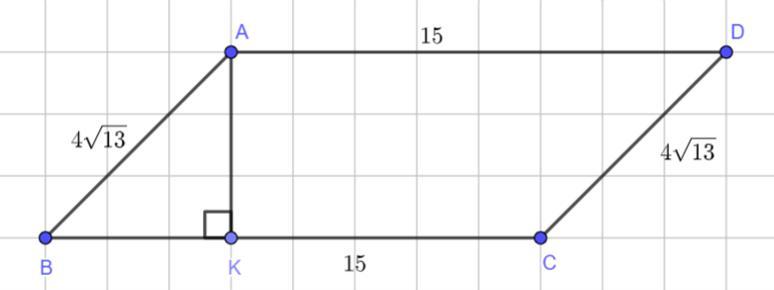
- Способ №2 (см. рисунок во вложении):
Проведем высоту параллелограмма AK и рассмотрим получившийся прямоугольный треугольник AKB.
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего ему катета к прилежащему, поэтому:
Катеты треугольника относятся как 2 : 3.
Пусть коэффициент пропорциональности равен x, тогда AK = 2x, BK = 3x, а по теореме Пифагора:
(2x)² + (3x)² = (4√13)²
4x² + 9x² = 16 · 13
13x² = 208
x² = 208 : 13
x² = 16 ⇒ x = 4.
AK = 2 · 4 = 8.
Найдем площадь параллелограмма, умножив его высоту на ту сторону, на которую она опущена:
(кв. единиц).
Ответ: 120.