Одна из сторон параллелограмма равна 12 другая равна 5, а тангенс одного из углов равен √2/4. Найти площадь

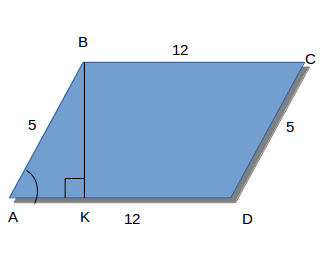
Дано: ABCD - паралелограмм; AB = 5(см); AD = 12(см) tgA = √2/2.

Найти S

                         Решение:

С вершины угла В проведём высоту ВК и получаем прямоугольный треугольник AKB

tg A - это отношение противолежащего катета к прилежащему, тоесть:

tg A = BK/ AK = √2/4

BK = √2 (см)

AK = 4 (см)

По т. Пифагора определяем гипотенузу

AB = √ (AK²+BK²) = √(4²+(√2)²)=√18

sin A = BK/AB = √2/√18 = 1/3

Отсюда площадь

S = AB * AD * sin A = 12*5*1/3 = 20 (см²).

Ответ: 20 (см²).