Один из острых углов прямоугольного треугольника равен 42⁰. Найдите угол между высотой и биссектрисой ,проведенными из вершины прямого угла треугольника.
(С ОБЪЯСНЕНИЕМ ПОЖАЛУЙСТА :3)
Ответы на вопрос
Ответил 3077108
0
Ответ:
3 градуса
Объяснение:
- Пусть СН - высота, СL - биссектриса в треугольнике ABC с прямым углом С
- Рассмотрим треугольник СВН: в нём угол СНВ = 90° - т.к. СН перпендикулярно АВ. Тогда угол НСВ = 180 - 90 - 42 = 48° (сумма углов треугольника равна 180°).
- угол СНL = угол НСВ - угол LСВ. Угол LCB = 90°/2 = 45° - т.к. CL - биссектриса прямого угла.
- тогда угол СНL = 48°-45° = 3°
Приложения:
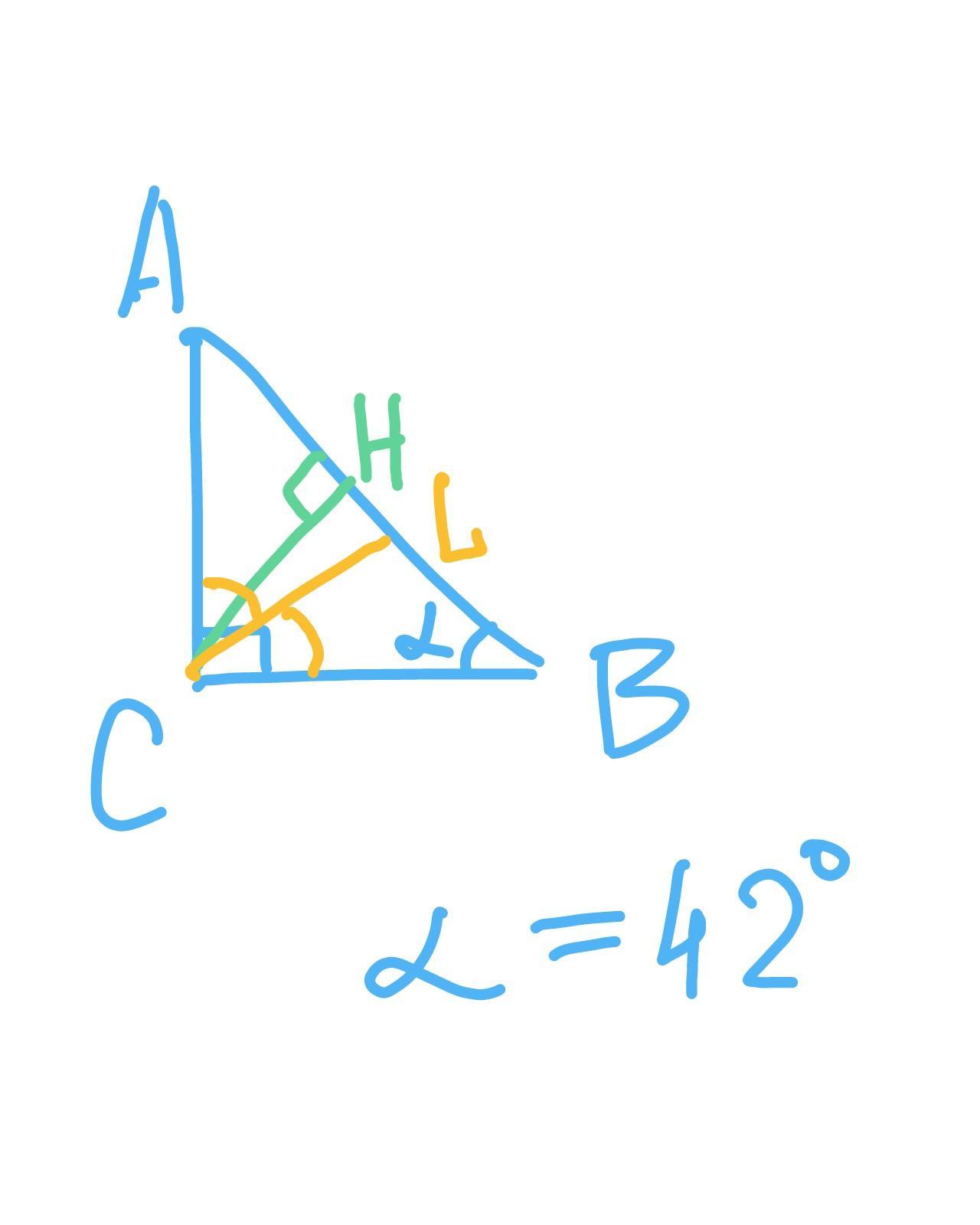
Новые вопросы
Математика,
1 год назад
География,
1 год назад
Литература,
6 лет назад
Алгебра,
6 лет назад
Физика,
8 лет назад