ОЧЕНЬ СРОЧНО
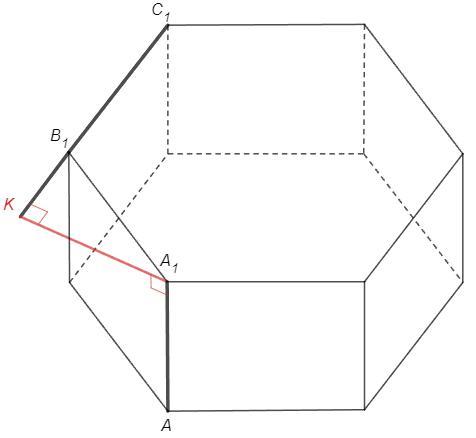
2.У правильной шестиугольной призмы АВСDEFА1В1С1D1E1F1 все ребра равны 1. Найти расстояние между прямыми АА1 и В1С1.​

Правильная призма

- прямая (боковые ребра перпендикулярны основаниям)

- в основаниях правильные многоугольники

Прямая AA1 пересекает плоскость A1B1C1 в точке, не лежащей на прямой B1C1 - прямые скрещиваются.

Расстояние между скрещивающимися прямыми - длина общего перпендикуляра.

Опустим перпендикуляр A1K на продолжение B1C1

AA1⊥(A1B1C1) => AA1⊥A1K

A1K - искомый общий перпендикуляр

∠A1B1K=60° (внешний угол правильного шестиугольника)

A1K =A1B1 sin60° =√3/2