Алгебра, вопрос задал vibindhv , 6 лет назад

ОЧЕНЬ ПОЖАЛУЙСТА ПОМОГИТЕ
ООУ добавить
1) log5(4-3x)=4log25 3+2
2) lg(2x^2+13)=2/log5 10
3) log1/3(5-x)-log3(-1-x)+3=0

Приложения:

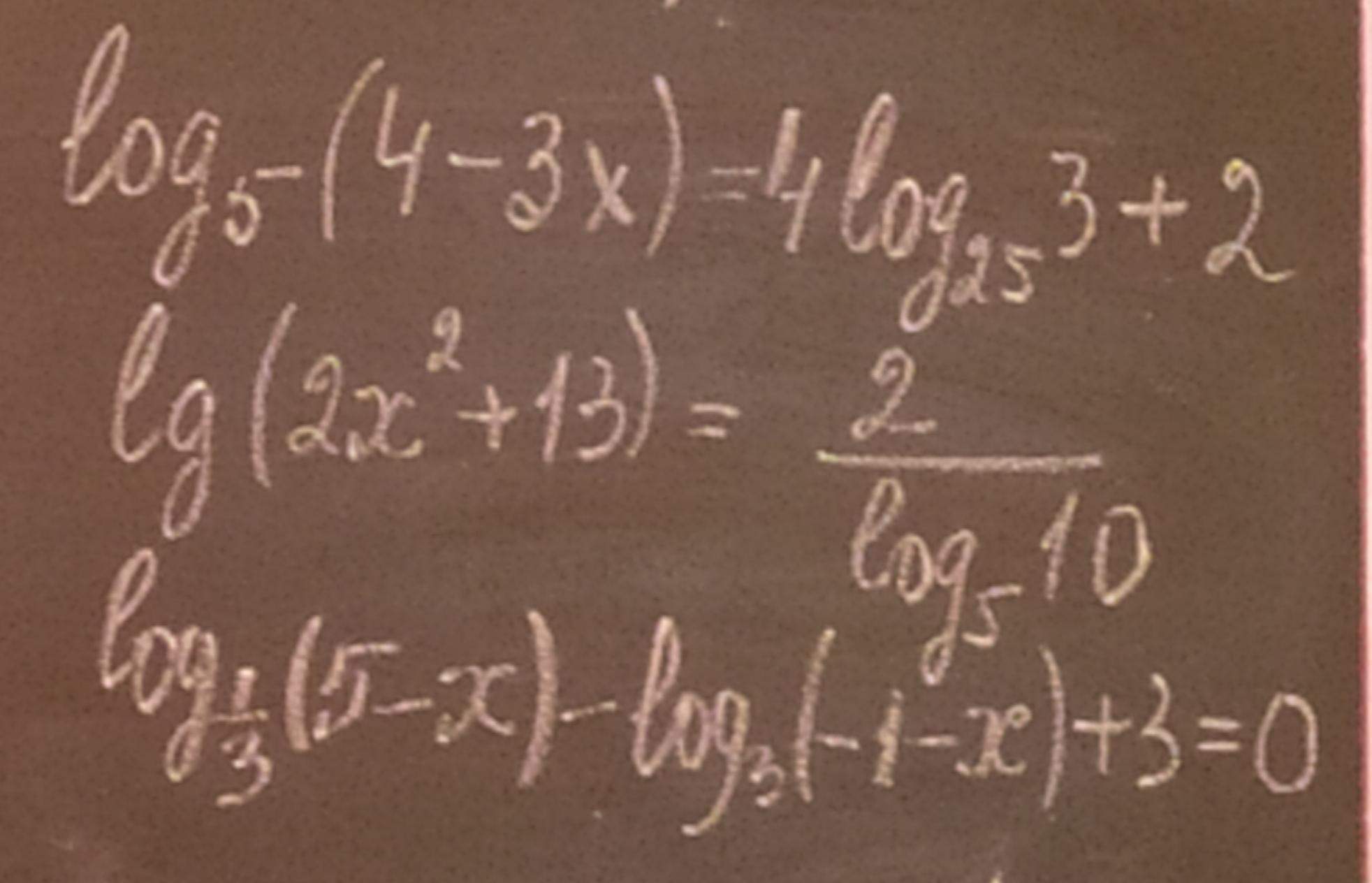
Ответы на вопрос

Ответил kapysva
1

Ответ:

1)

- 73 \frac{2}{3}

2)

\sqrt{6} \\ - \sqrt{6}

3) -4

Объяснение:

1)

log_{5}(4 - 3x) = 4 log_{25}(3) + 2

log_{5}(4 - 3x) = 4 log_{ {5}^{2} }(3) + 2 log_{5}(5)

log_{5}(4x - 3) = 4 \times \frac{1}{2} log_{5}(3) + log_{5}( {5}^{2} )

log_{5}(4 - 3x) = 2 log_{5}(3) + log_{5}(25)

log_{5}(4 - 3x) = log_{5}( {3}^{2} ) + log_{5}(25)

log_{5}(4 - 3x) = log_{5}(9) + log_{5}(25)

log_{5}(4 - 3x) = log_{5}(9 \times 25)

log_{5}(4 - 3x) = log_{5}(225)

4 - 3x > 0 \\ 3x < 4 \\ x < \frac{4}{3} \\ x < 1 \frac{1}{3}

4 - 3x = 225 \\ 3x = - 221 \\ x = \frac{ - 221}{3} = - 73 \frac{2}{3}

2)

log_{10}(2 {x}^{2} + 13 ) = \frac{2}{ log_{5}(10) }

log_{10}(2 {x}^{2} + 13) = 2 \times \frac{1}{ \frac{1}{ log_{10}(5) } }

log_{10}(2 {x}^{2} + 13) = 2 log_{10}(5)

log_{10}(2 {x}^{2} + 13 ) = log_{10}( {5}^{2} )

log_{10}(2 {x}^{2} + 13) = log_{10}(25)

2 {x}^{2} + 13 > 0

х є R

2 {x}^{2} + 13 = 25

2 {x}^{2} = 12

{x}^{2} = 6

x1 = \sqrt{6} \\ x2 = - \sqrt{6}

3)5-х>0

х<5

-1-х>0

х<-1

log_{ \frac{1}{3} }(5 - x) - log_{3}( - 1 - x) + 3 = 0

log_{ {3 }^{ - 1} }(5 - x) - log_{3}( - 1 - x) + 3 log_{3}(3) = 0

- log_{3}(5 - x) - log_{3}( - 1 - x) + log_{3}( {3}^{3} ) = 0

- log_{3}(5 - x) - log_{3}( - 1 - x) + log_{3}(27) = 0

- (log_{3}( - 1 - x) + log_{3}(5 - x) ) + log_{3}(27) = 0

- log_{3}(( - 1 - x)(5 - x)) + log_{3}(27) = 0

log_{3}(27) = log_{3}(( - 1 -x )(5 - x))

27 = ( - 1 - x)(5 - x)

- 5 + x - 5x + {x}^{2} = 27

{x}^{2} - 4x - 32 = 0

По теореме Виета:

x1 = - 4 \\ x2 = 8

х=8 не входит в промежуток возможных х, который написан с самого начала, поетому

х=-4

Предыдущий вопрос
Следующий вопрос
Новые вопросы