Объясните, пожалуйста, на понятном языке)
Приложения:
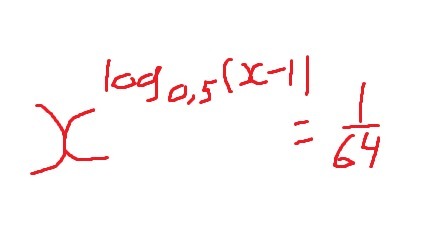
Ответы на вопрос
Ответил sedinalana
0
ОДЗ
{x>0
{x≠1
гарифмируете обе части уравнения по основанию0,5
log(0,5)(x^(log(0,5)x-1)=log(0,5)(1/64)
по свойству логарифма
(log(0,5)x)(log(0,5)x-1)=6
log(0,5)x=а
а²-a=6
a²-a-6=0
a1+a2=1 U a1*a2=-6
a1=-2
log(0,5)x=-2⇒x=4
a2=3
log(0,5)x=3⇒x=1/8
x1=1/8
x2=4
{x>0
{x≠1
гарифмируете обе части уравнения по основанию0,5
log(0,5)(x^(log(0,5)x-1)=log(0,5)(1/64)
по свойству логарифма
(log(0,5)x)(log(0,5)x-1)=6
log(0,5)x=а
а²-a=6
a²-a-6=0
a1+a2=1 U a1*a2=-6
a1=-2
log(0,5)x=-2⇒x=4
a2=3
log(0,5)x=3⇒x=1/8
x1=1/8
x2=4
Ответил XGuruX
0
так все-таки, ответы в конце совпадают.. Я прям точь в точь из учебника все взял
Ответил oganesbagoyan
0
Sedinalana решила не тот пример , что Вы предлагали а именно x ^ Log₀,₅ ( x- 1 ) = 4⁻³ , а другой x ^ ( Log₀,₅ x- 1 ) = 4⁻³ * * * [ корректировала , а что делать ]
Ответил XGuruX
0
Скорее всего я допустил ошибку, а Sedina решила все верно. Вот так в учебнике условие выглядит: http://s019.radikal.ru/i635/1612/5c/8f7e6681c88d.png
Ответил oganesbagoyan
0
В учебнике условие x ^ ( Log₀,₅ x- 1 ) = 1 /64 , а не то что Вы переписали ошибочно x ^ Log₀,₅( x- 1 ) = 1 /64
Ответил XGuruX
0
А к сожалению, теперь нельзя вопрос изменить, хотя при этом ответ правильный...
Новые вопросы