Обчисліть площу криволінійної трапеції, обмеженої графіком функції y=3x^2 і прямими y=0, x=1, x=2

Ответ:  7 кв. ед.

Объяснение:

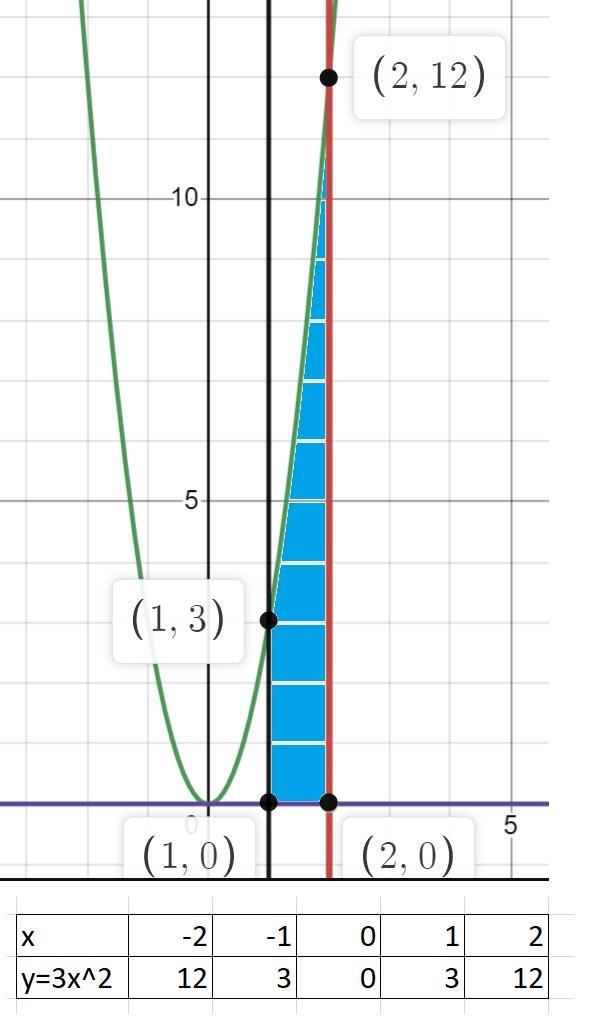
Обчисліть площу криволінійної трапеції, обмеженої графіком функції Строим графики функций  y=3x^2;  y=0;  x=1; x=2. (См. скриншот).

Площадь S = ∫(a;b)f(x)dx.

Пределы интегрирования a = 1;  b =2.

f(x) = 3x^2.  Тогда

S =∫(1;2)(3x^2)dx = 3∫(1;2) (x^2)dx = 3 x^3/3|(1;2) = (2^3-1^3) = 8-1 = 7 кв. ед.