Математика, вопрос задал odindvatri , 8 лет назад

НУЖНО СРОЧНО РЕШИТЬ ПОМОГИТЕ ПЛС

Приложения:

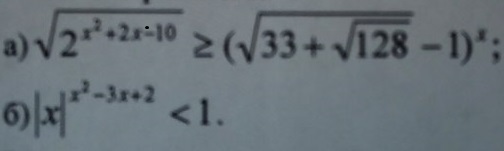
Ответы на вопрос

Ответил gartenzie

а) Извлекаем вложенный радикал:    $sqrt{ 33 + sqrt{ 64 cdot 2 } } .$

Пусть:    $sqrt{ 33 + 8 sqrt{2} } = a + b sqrt{2} , { a , b } in Q$     (рациональные числа)

Тогда:    $33 + 8 sqrt{2} = ( a + b sqrt{2} )^2 .$

$33 + 8 sqrt{2} = a^2 + 2ab sqrt{2} + 2b^2 ;$

$left{begin{array}{l} a^2 + 2b^2 = 33 , \ left|begin{array}{l} 2ab sqrt{2} = 8 sqrt{2} , \ 2ab = 8 , \ ab = 4 , \ b = frac{4}{a} ; end{array}right end{array}right$

$a^2 + 2 ( frac{4}{a} )^2 = 33 ;$

$a^2 + 2 cdot frac{16}{a^2} - 33 = 0 ; || cdot a^2 ;$

$(a^2)^2 - 33 a^2 + 32 = 0 ;$

$D = 33^2 - 4 cdot 32 = 33^2 - 33 - 32 - 32 - 31 = 31^2 ;$

$a^2 = frac{ 33 pm 31 }{2} in { 1 , 32 } ;$

Выбираем значение, являющееся целым квадратом:

$a = 1 ;$

$b = frac{4}{a} = 4 ;$

$sqrt{ 33 + 8 sqrt{2} } = 1 + 4 sqrt{2} ;$

Проверим: $( 1 + 4 sqrt{2} )^2 = 1^2 + 2 cdot 1 cdot 4 sqrt{2} + ( 4 sqrt{2} )^2 =$

$= 1 + 8 sqrt{2} + 16 cdot 2 = 1 + sqrt{ 8^2 cdot 2 } + 32 = 33 + sqrt{128}$     – всё верно.

Перепишем исходное неравенство:

$sqrt{ 2^{ x^2 + 2x -10 } } geq ( sqrt{ 33 + sqrt{128} } - 1 )^x ;$

$sqrt{ 2^{ x^2 + 2x -10 } } geq ( [ 1 + 4 sqrt{2} ] - 1 )^x ;$

$sqrt{ 2^{ x^2 + 2x -10 } } geq ( 4 sqrt{2} )^x ;$

Обе части уравнения – положительны, так что мы перейдём к эквивалентному уравнению при возведении обеих его частей в квадрат:

$2^{ x^2 + 2x -10 } geq ( ( 4 sqrt{2} )^x)^2 ;$

$2^{ x^2 + 2x -10 } geq ( 4 sqrt{2} )^{2x} ;$

$2^{ x^2 + 2x -10 } geq ( ( 2^2 sqrt{2} )^2 )^x ;$

$2^{ x^2 + 2x -10 } geq ( (2^2)^2 ( sqrt{2} )^2 )^x ;$

$2^{ x^2 + 2x -10 } geq ( 2^4 cdot 2 )^x ;$

$2^{ x^2 + 2x -10 } geq ( 2^5 )^x ;$

$2^{ x^2 + 2x -10 } geq 2^{5x} ;$

$x^2 + 2x -10 geq 5x ;$

$x^2 - 3x -10 geq 0 ;$

$D = 3^2 - 4 cdot (-10) = 9 + 40 = 49 = 7^2 ;$

$x_{1,2} = frac{ 3 pm 7 }{2} in { -2 ; 5 } ;$

О т в е т :    $x in ( -infty ; -2 ] cup [ 5 ; +infty ) ;$

б)

$|x|^{ x^2 - 3x + 2 } leq 1 ;$

[I] При:    $x = 0 ; Rightarrow |0|^{ 0^2 - 3 cdot 0 + 2 } = |0|^2 = 0 < 1$
неравенство удовлетворено:    $x = 0 ;$

[II] При:    $x = 1 ; Rightarrow |1|^{ 1^2 - 3 cdot 1 + 2 } = 1^0 = 1 = 1$
неравенство НЕ удовлетворено:    $x neq 1 ;$

[III] При:    $0 < |x| < 1 ; Rightarrow | frac{1}{x} | > 1 ;$

$|x|^{ x^2 - 3x + 2 } leq |x|^0 ; Rightarrow |frac{1}{x}|^{ x^2 - 3x + 2 } geq |frac{1}{x}|^0$

$x^2 - 3x + 2 geq 0 ;$

$D = 3^2 - 4 cdot 2 = 1 = 1^2 ;$

$x_{1,2} = frac{ 3 pm 1 }{2} in { 1 , 2 } ;$

$x in ( ( -1 ; 0 ) cup ( 0 ; 1 ) ) ;$

[IV] При:    $|x| > 1 ;$

$|x|^{ x^2 - 3x + 2 } leq |x|^0 ;$

$x^2 - 3x + 2 leq 0 ;$

$D = 3^2 - 4 cdot 2 = 1 = 1^2 ;$

$x_{1,2} = frac{ 3 pm 1 }{2} in { 1 , 2 } ;$

$x in ( 1 ; 2 ) ;$

Объединяем случаи: [I], [II], [III] и [IV].

О т в е т :    $x in ( ( -1 ; 1 ) cup ( 1 ; 2 ) ) equiv ( -1 ; 2 )/{1} ;$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

География, 2 года назад

Води суходолу Південої Америки...

Химия, 2 года назад

ПОМОГИТЕ ПОЖАЛУЙСТА ХИМИЯ УРАВНЕНИЯ...

Литература, 8 лет назад

написать краткий рассказ чебурашка...

Геометрия, 8 лет назад

В прямоугольном треугольнике АВС с гипотинузой АВ внешный угол при вершине.В равен 150°,АС+АВ=12см.Найдите длину гмпотенузы треугольника.

Алгебра, 9 лет назад

Найти первообразную (1-2х)³. Помогите пожалуйста :)...

Информатика, 9 лет назад

Создать файл содержащий структуру записи человек: пол, имя, рост. Вывести на экран средний женский рост и имя самого высокого мужчины...