НУЖНО СРОЧНО Основою піраміди є прямокутник зі сторонами 18см і 32см. Основою висоти піраміди є точка перетину діагоналей прямокутника. Знайдіть площу бічної поверхні піраміди, якщо її висота =12см
zmeura1204:
Напишіть щось.
Ответы на вопрос
Ответил zmeura1204
3
Ответ:
Площа бічної поверхні піраміди дорівнює 840см²
Объяснение:
ОК=½*ВС=½*32=16см
∆∆SOK- прямокутний трикутник
Теорема Піфагора:
SK=√(SO²+OK²)=√(12²+16²)=
=√(144+256)=√400=20см
S(∆SCD)=½*SK*CD=½*20*18=
=180см²
∆SCD=∆SAB
OM=½*AB=½*18=9см
∆SOM- прямокутний трикутник
Теорема Піфагора:
SM=√(SO²+OM²)=√(12²+9²)=
=√(144+81)=√225=15см
S(∆SAD)=½*SM*AD=
=½*15*32=240см²
∆SAD=∆SBC
Sб=2*S(∆SAD)+2*S(∆SCD)=
=2*240+2*180=480+360=840см²
Приложения:
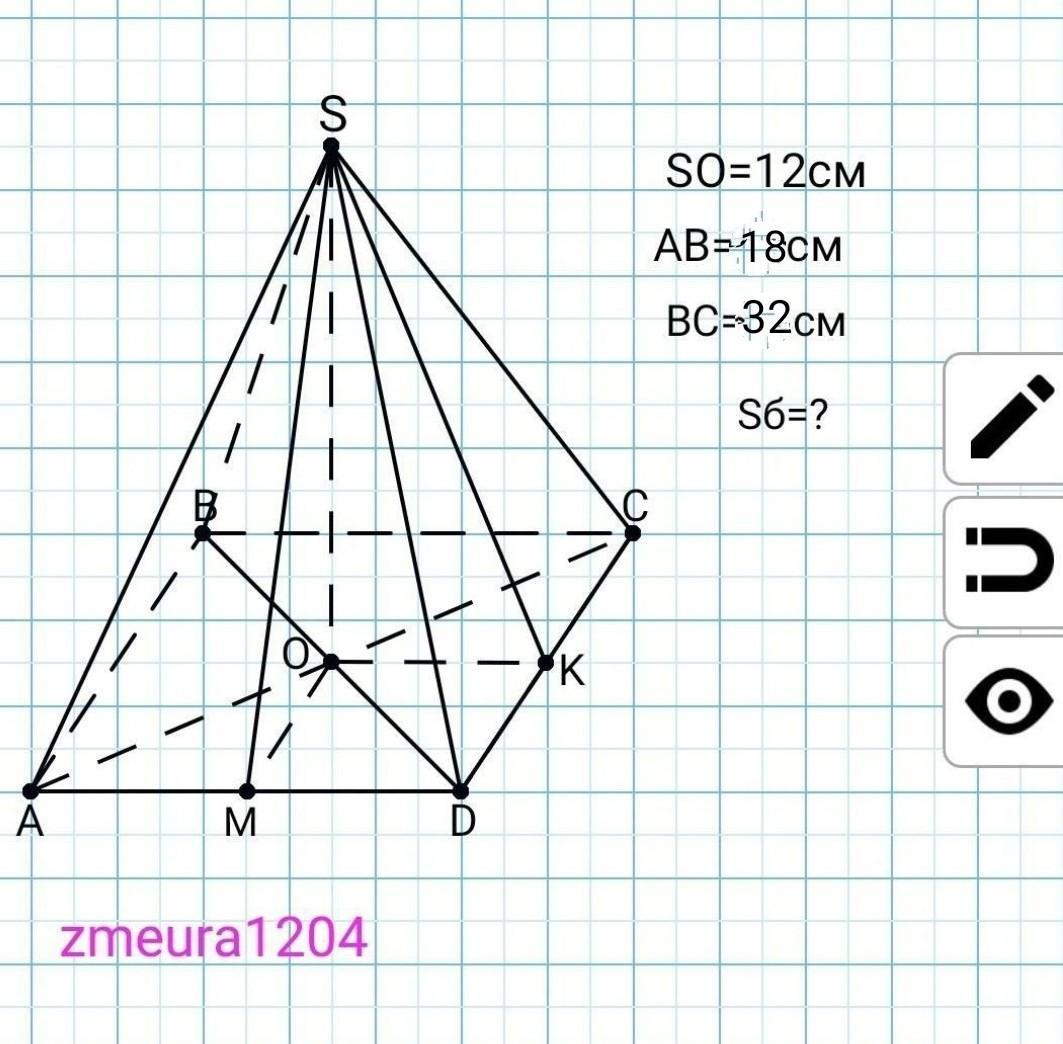
ДАЮ 100 БАЛЛОВ УМОЛЯЮ ПОМОГИТЕ С ГЕОМЕТРИЕЙ 9 КЛАС
Новые вопросы
Английский язык,
11 месяцев назад
Українська мова,
11 месяцев назад
Английский язык,
11 месяцев назад
Математика,
11 месяцев назад
Биология,
6 лет назад