Математика, вопрос задал kotiklikol , 7 месяцев назад

Нужно решить методом интегрирования – подведение переменной под знак дифференциала. Всё расписать

Приложения:

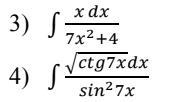
Ответы на вопрос

Ответил Alnadya

Ответ:

Интегрирование мeтодом подведения под знак дифференциала .

$\bf \displaystyle 3)\ \ \int \frac{x\, dx}{7x^2+4}=\Big[\ d(7x^2+4)=14x\, dx\, \Big]=\frac{1}{14}\int \frac{d(7x^2+4)}{7x^2+4}=\\\\\\=\Big[\ \int \frac{du}{u}=ln|u|+C\, \Big]=\frac{1}{14}\cdot ln|7x^2+4|+C$

$\bf \displaystyle 4)\ \ \int \frac{\sqrt{ctg7x}\, dx}{sin^27x}=\Big[\ d(ctg7x)=-\frac{7\, dx}{sin^27x}\, \Big]=-\frac{1}{7}\int \sqrt{ctg7x}\cdot d(ctg7x)=\\\\\\=\Big[\ \int \sqrt{u}\, du=\frac{2\, u^{\frac{3}{2}}}{3}+C\, \Big]=-\frac{2}{21}\cdot \sqrt{ctg^37x}+C$

Приложения:

Предыдущий вопрос

Следующий вопрос

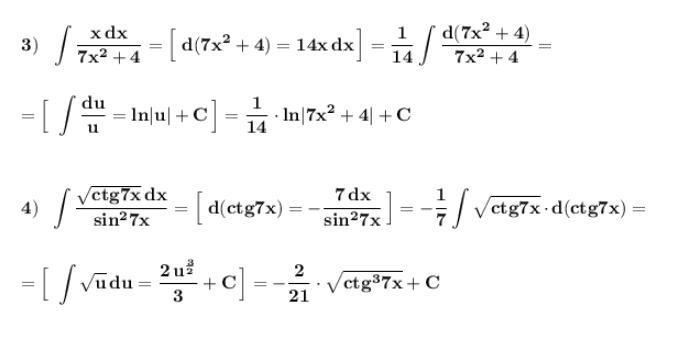
Новые вопросы

Математика, 4 месяца назад

как будет 2 + 2???????

Геометрия, 4 месяца назад

Найдите площадь равнобедренного треугольника, если боковая сторона равна 4 см, а основание - 6 см СРОЧНО ПОМОГИТЕ ПОЖАЛУЙСТА УМАЛЯЮ!!!! СПАМ-БАН!!!!!

Литература, 7 месяцев назад

детальная информация по поэмы "Полтава" Пушкина...

Геометрия, 7 месяцев назад

МОЛЮ ДОПОМОЖІТЬ!!!На рисунку зображено куб АBCDA1B1C1,. Пряма...

Алгебра, 6 лет назад

Пожалуйста срочно!!(((...

Физика, 6 лет назад

дуже прошу розв'язати на фотографії, даю багато балів + оцінку високу кулька масою 10 г вилітає з пружинного пістолета, влучає в центр підвішеного на нитках пластилінового бруска масою 30 г і...