Алгебра, вопрос задал anastasia063rus , 6 лет назад

Нужно полное решение. Найдите производную функции (на фото) в точке x0 = 2.

Приложения:

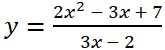
Ответы на вопрос

Ответил natalyabryukhova

Объяснение:

$\displaystyle (\frac{u}{v})'=\frac{u'v-uv'}{v^2}$

$\displaystyle y=\frac{2x^2-3x+7}{3x-2} \\\\y'=\frac{(2*2x-3)*(3x-2)-(2x^2-3x+7)*3}{(3x-2)^2} =\frac{12x^2-8x-9x+6-6x^2+9x-21}{(3x-2)^2} =\\\\=\frac{6x^2-8x-15}{(3x-2)^2}$

$\displaystyle x_0=2$

$\displaystyle y'(2)=\frac{6*4-8*2-15}{(3*2-2)^2} =\frac{-7}{16}=-\frac{7}{16}$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Алгебра, 1 год назад

Найдите длину солнечной тени от здания высотой 11,7 м,если солнечная тень от человека ростом 1,8 м равна 2 м. Ответ укажите в метрах.

Математика, 1 год назад

Начерти отрезок и луч, который его пересекает.Сколько стало отрезков?Сколько лучей?

История, 6 лет назад

Кто первый император в Франции в годы правления императора Наполеона?

Математика, 6 лет назад

11. Найдите все первообразные для функции: 1 а) 200, б) x-200. г) х"; д) х 1 в) е) x х...

Математика, 8 лет назад

Помогите пожалуйста.Номер 635.

Литература, 8 лет назад

Срочно мне нужно краткое содержание рассказа Ночь перед Рождеством!! Заранее спасибо)!