Нужно найти площадь равнобедренной трапеции.С РИСУНКОМ!!!
Ответы на вопрос
Ответил Grib000089522114811
0
Сначала нужно вычислить длину высоты трапеции, для этого:
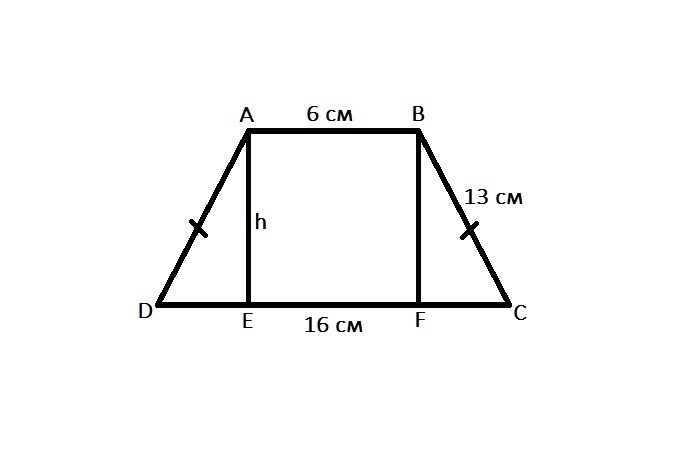
Надо воспользоваться теоремой Пифагора для одного из боковых треугольников(теорема Пифагора- Квадрат гипотенузы равен сумме квадратов катетов). Но нам известен только один катет треугольника, поэтому необходимо найти второй: по рисунку видно, что две высоты вместе с верхним основанием образовывают прямоугольник. По свойству прямоугольника, его противоположные стороны равны между собой, поэтому часть нижнего основания равна 6 см. Помимо этой части есть ещё два одинаковых катета от двух одинаковых треугольников. Чтобы вычислить один катет, нам надо из всего нижнего основания вычесть известную часть 6 см, поучится 10 см, а поскольку у нас два одинаковых катета, нам просто нужно 10 см разделить на 2, равно 5 см- второй катет треугольника.
Применяем теорему Пифагора h^2=AD^2-DE^2, откуда h=корень(13^2-5^2) h=12 см( мы нашли высоту трапеции)
Ну наконец! Последнее действие: применяем формулу для нахождения площади равнобедренной трапеции S=(AB+CD)*h/2
S=(6 см+16 см)*12 см/2=132 см*2
Решение:
1)16-6=10 см
2)10/2=5 см
3)h^2=AD^2-DE^2=(т.Пифагора)
4)S=(AB+CD)*h/2=(6 см+16 см)*12 см/2=132 см^2
Ответ: S трапеции=132 см^2
Надо воспользоваться теоремой Пифагора для одного из боковых треугольников(теорема Пифагора- Квадрат гипотенузы равен сумме квадратов катетов). Но нам известен только один катет треугольника, поэтому необходимо найти второй: по рисунку видно, что две высоты вместе с верхним основанием образовывают прямоугольник. По свойству прямоугольника, его противоположные стороны равны между собой, поэтому часть нижнего основания равна 6 см. Помимо этой части есть ещё два одинаковых катета от двух одинаковых треугольников. Чтобы вычислить один катет, нам надо из всего нижнего основания вычесть известную часть 6 см, поучится 10 см, а поскольку у нас два одинаковых катета, нам просто нужно 10 см разделить на 2, равно 5 см- второй катет треугольника.
Применяем теорему Пифагора h^2=AD^2-DE^2, откуда h=корень(13^2-5^2) h=12 см( мы нашли высоту трапеции)
Ну наконец! Последнее действие: применяем формулу для нахождения площади равнобедренной трапеции S=(AB+CD)*h/2
S=(6 см+16 см)*12 см/2=132 см*2
Решение:
1)16-6=10 см
2)10/2=5 см
3)h^2=AD^2-DE^2=(т.Пифагора)
4)S=(AB+CD)*h/2=(6 см+16 см)*12 см/2=132 см^2
Ответ: S трапеции=132 см^2
Приложения:
Новые вопросы
Химия,
2 года назад
Биология,
7 лет назад
Геометрия,
7 лет назад
Математика,
8 лет назад
Информатика,
8 лет назад