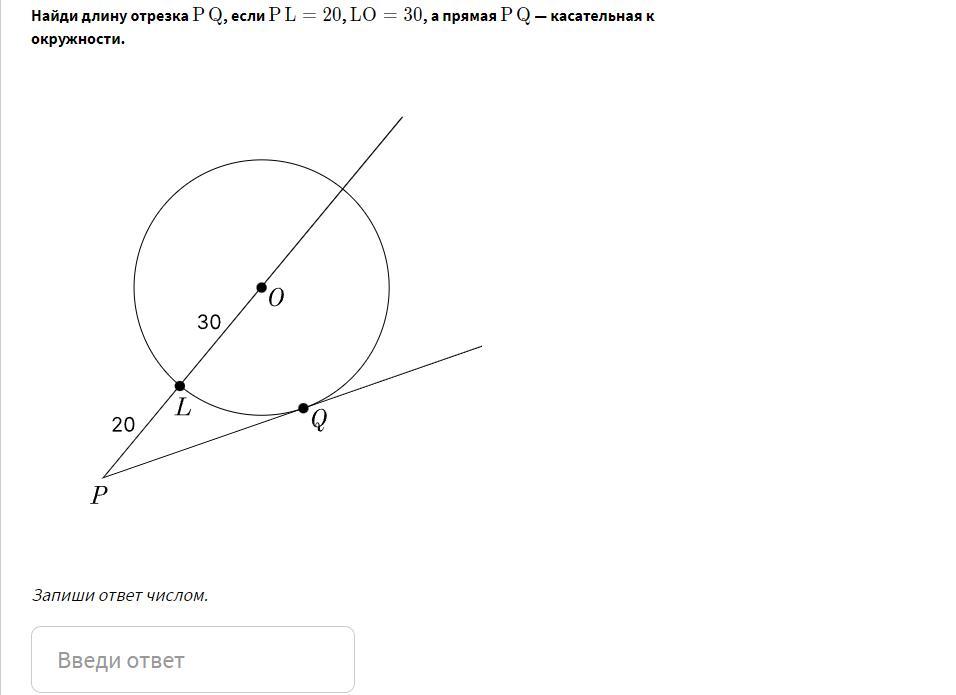
Нужна помощь, срочно. Найди длину отрезка PQ , если PL =20 , LO =30 , а прямая PQ — касательная к окружности.

Ответ:

Отрезок PQ равен 40 ед

Объяснение:

Дана окружность с центром в точке О. PL =20 , LO =30 , прямая PQ — касательная к окружности.Найти PQ.

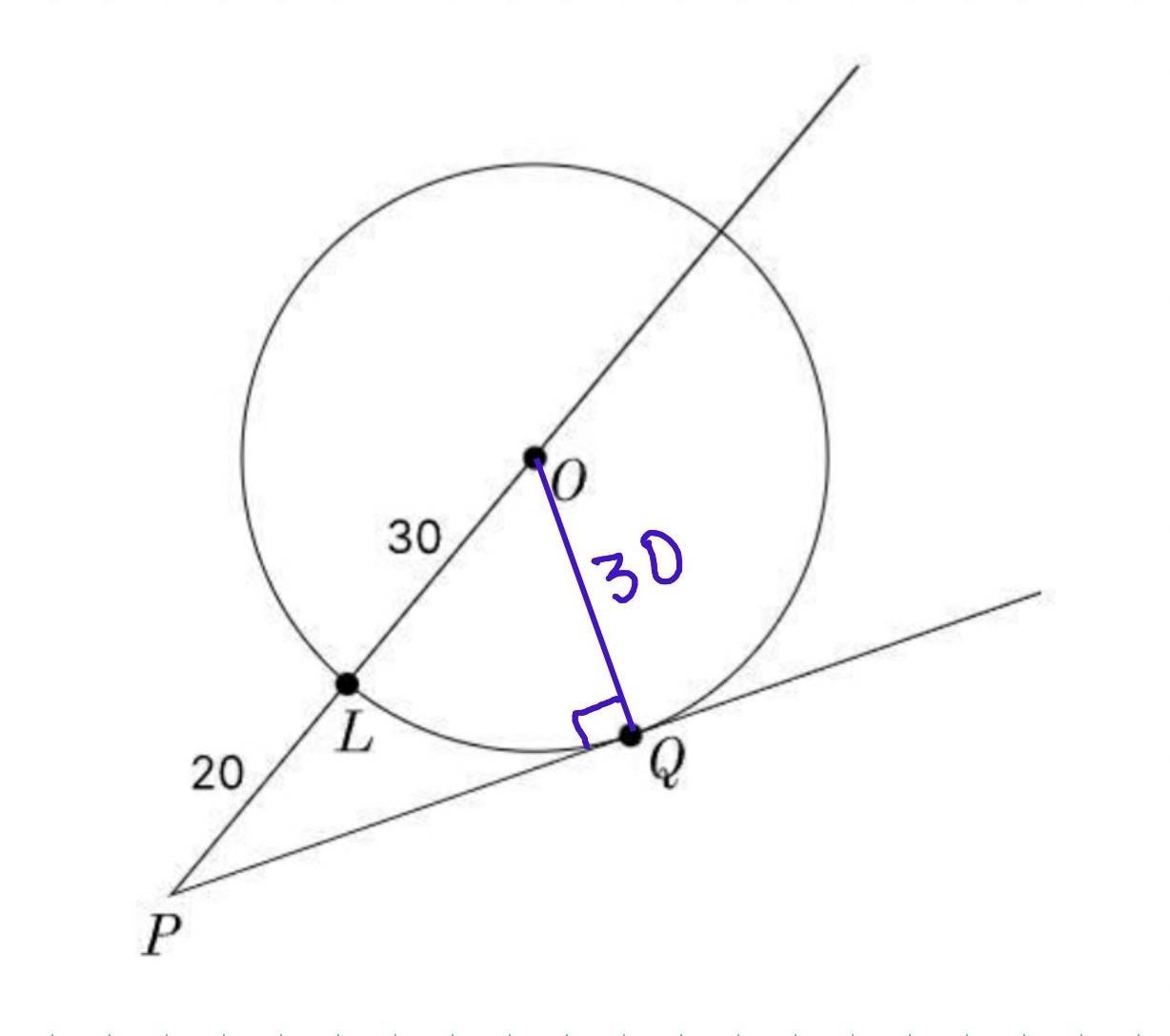
PQ - касательная к окружности. Проведём радиус окружности из центра в точке О в точку касания Q.

Свойство касательной: касательная к окружности перпендикулярна радиусу, проведенному в точку касания.

Следовательно PQ⟂OQ, △OQP - прямоугольный, ∠Q=90°.

OQ=OL=30 ед, как радиусы окружности. PO = PL + LO = 20+30=50 ед.

Из прямоугольного треугольника OQP по теореме Пифагора найдём катет PQ.

PQ²=PO²-OQ²=50²-30²=2500-900=1600

PQ=√1600=40 ед.

Длина отрезка PQ=40ед.