Алгебра, вопрос задал 12assua12 , 6 лет назад

Нужна помощь 35 баллов

Приложения:

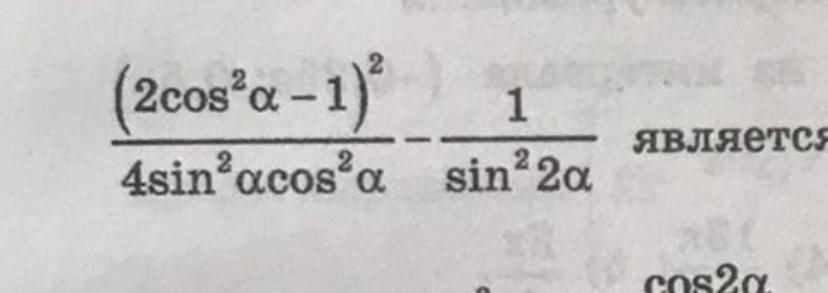
Ответы на вопрос

Ответил Universalka

$\displaystyle\bf\\\frac{(2Cos^{2} \alpha -1)^{2} }{4Sin^{2} \alpha cos^{2} \alpha } -\frac{1}{Sin^{2}2\alpha } =\frac{(Cos2\alpha )^{2} }{(2Sin\alpha Cos\alpha )^{2} } -(1+Ctg^{2} 2\alpha) =\\\\\\=\frac{Cos^{2}2\alpha }{Sin^{2} 2\alpha } -1-Ctg^{2} 2\alpha =Ctg^{2}2\alpha -1-Ctg^{2} 2\alpha =-1$

При решении были применены формулы :

$\displaystyle\bf\\1)\\2Cos^{2}\alpha -1=Cos2\alpha \\\\2)\\2Sin\alpha Cos\alpha =Sin2\alpha \\\\3)\\\frac{1}{Sin^{2}\alpha } =1+Ctg^{2}\alpha \\\\4)\\\frac{Cos\alpha }{Sin\alpha }=Ctg\alpha$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Здравствуйте, можете пожалуйста назвать все виды служебных слов. Заранее спасибо...

Английский язык, 1 год назад

ПОМОГИТЕ ПОЖАЛУЙСТА ПРОШУ ВАС ОЧЕНЬ НУЖНО ДО ЗАВТРА . Измените предложения , употребив конструкцию to, have, got. à) Образец: We have a large family. We ve got a large family. He has a...

Биология, 6 лет назад

В каком предложении оба выделенных слова пишутся раздельно? 1 По-особенному сияли на праздничной ёлке (НЕ)КУПЛЕННЫЕ игрушки-поделки, (НЕ)ЗАВЁРНУТЫЕ даже в фольгу. 2 Почему внимание (НЕ)ПРОШЕНЫХ...

Русский язык, 6 лет назад

78. Прочитайте. 1. Рыба-ремень длинная 2. Иной раз раз достигает девяти метров. 3. Ну и ремешок! 4. Эту серебристо-розо- вую рыбу салой короной на голове ещё называют сельдяным королём. 5. А уж так...

История, 8 лет назад

Причины советско- финской войны. Помогитеее!

Информатика, 8 лет назад

Объем статьи, набранный на компьютере, составляет 48 килобайт Определите сколько страниц содержит статья , если известно что на каждой странице 48 строк В каждой строке 64 символа Каждый символ...