Номер 975 и 958 (в).
Приложения:


Ответы на вопрос
Ответил mefody66
0
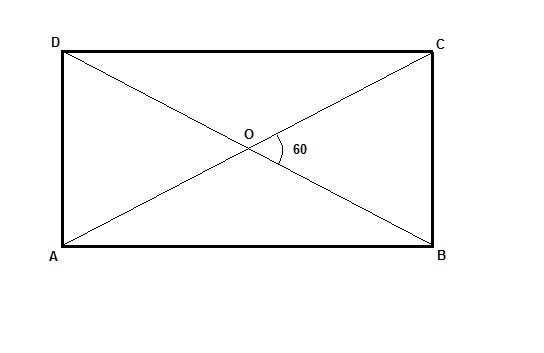
958 в) Очевидно, AO = BO = CO = DO.
Треугольники AOB, BOC, COD, AOD равнобедренные, а так как
AOD = BOC = 60°, то AOD и BOC - равносторонние. AO = AD = BC.
Дальше возможно 2 варианта.
1) Короткая сторона равна AD = BC = AO = 18.
Но AO - это радиус описанной окружности. R = AO = 18.
Длина окружности C = 2pi*R = 2pi*18 = 36pi.
2) Длинная сторона равна 18, короткая равна а.
Треугольник AOB - равнобедренный с углами 120°, 30°, 30°.
По теореме косинусов в треугольнике AOB
AB^2 = AO^2 + OB^2 - 2*AO*OB*cos AOB
18^2 = a^2 + a^2 - 2a*a*(-1/2) = 2a^2 + a^2 = 3a^2
a^2 = 18^2/3; a = 18/√3 = 18√3/3 = 6√3 = AO
Опять же, AO - это радиус описанной окружности, R = AO = 6√3.
C = 2pi*R = 2pi*6√3 = 12pi*√3
975. Длина дуги через центральный угол a (радиан) и радиус R:
L = R*a
Если L = R, то угол а = 1 радиан.
Треугольники AOB, BOC, COD, AOD равнобедренные, а так как
AOD = BOC = 60°, то AOD и BOC - равносторонние. AO = AD = BC.
Дальше возможно 2 варианта.
1) Короткая сторона равна AD = BC = AO = 18.
Но AO - это радиус описанной окружности. R = AO = 18.
Длина окружности C = 2pi*R = 2pi*18 = 36pi.
2) Длинная сторона равна 18, короткая равна а.
Треугольник AOB - равнобедренный с углами 120°, 30°, 30°.
По теореме косинусов в треугольнике AOB
AB^2 = AO^2 + OB^2 - 2*AO*OB*cos AOB
18^2 = a^2 + a^2 - 2a*a*(-1/2) = 2a^2 + a^2 = 3a^2
a^2 = 18^2/3; a = 18/√3 = 18√3/3 = 6√3 = AO
Опять же, AO - это радиус описанной окружности, R = AO = 6√3.
C = 2pi*R = 2pi*6√3 = 12pi*√3
975. Длина дуги через центральный угол a (радиан) и радиус R:
L = R*a
Если L = R, то угол а = 1 радиан.
Приложения:
Новые вопросы
История,
2 года назад
История,
2 года назад
Математика,
8 лет назад
Математика,
8 лет назад
Математика,
9 лет назад