номер 2.2 .2.3 пжжжжжжж помогите
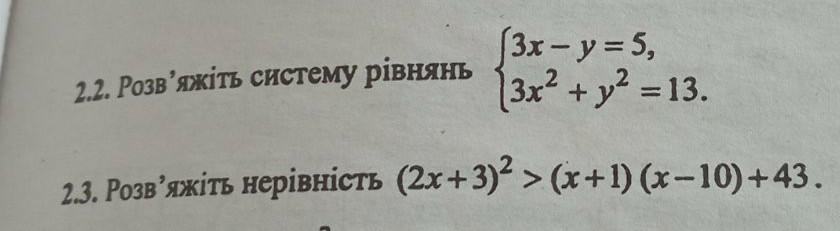
Ответы на вопрос
Ответ:
2.2. (x₁; y₁) = (0,5; -3,5)
(x₂; y₂) = (2; 1)
2.3. (-∞; -8) U (1; +∞)
Объяснение:
2.2. Решим систему уравнении.
Выразим из первого уравнения у:
Подставим у во второе уравнение:
3х² + (3x - 5)² = 13
3х² + 9х² - 30х + 25 = 13
12х² - 30х + 12 = 0 | :6
2х² - 5х + 2 = 0
D = 25 - 4 * 2 * 2 = 9
Подставим х и найдем у:
y₁ = 3 * 0,5 - 5 = 1,5 - 5 = -3,5
y₂ = 3 * 2 - 5 = 6 - 5 = 1
Ответ: (x₁; y₁) = (0,5; -3,5)
(x₂; y₂) = (2; 1)
2.3. (2x + 3)² > (x + 1)(x - 10) + 43
4x² + 12x + 9 > x² - 10x + x - 10 + 43
3x² + 21x - 24 > 0
Нули функции:
3x² + 21x - 24 = 0
D = 441 - 4 * 3 * (-24) = 729
Решим неравенство методом интервалов:
3x² + 21x - 24 > 0
-------------------------◯--------------------------------------◯---------------------------->x
Выберем интервалы, где неравенство принимает положительные значения и запишем ответ.
Ответ: (-∞; -8) U (1; +∞)