Невесомая нить, перекинутая через блок в виде

сплошного однородного цилиндра, соединяет два

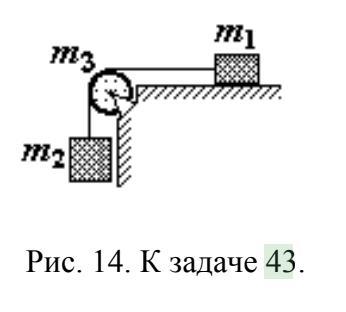
тела m1 = 0,50 кг и m2 = 0,90 кг. Масса цилиндра

m3 = 0,20 кг (рис. 14). Коэффициент трения тела

массой m1, скользящего по горизонтальной

поверхности стола, μ = 0,20. Рассчитать силы

натяжения нити Т1 и Т2 по обе стороны блока, а

также величину а ускорения этих тел.

Ответ: Т1 = 3,6 Н ;Т2 = 4,1 Н ; а = 5,2 м/с2.
P.S: Необходимо решение.

Ответ:

Т₁ ≈ 3,6 Н;      Т₂ ≈ 4,1 Н;      а ≈ 5,2 м/с².

Объяснение:

m₁ = 0.5 кг

m₂ = 0.9 кг

m₃ = 0.2 кг

g = 9.81 м/с²

μ = 0,2

----------------------------

а - ?    Т₁ - ?   Т₂ - ?

---------------------------

2-й закон Ньютона для тела 1

m₁a = T₁ - Fтр

Fтр = m₁gμ

тогда

m₁a = T₁ - m₁gμ            (1)

2-й закон Ньютона для тела 2

m₂a = m₂g - T₂              (2)

Для блока 3 имеем

J₃ε = T₂R - T₁R

Момент инерции сплошного цилиндра

J₃ = 0.5m₃R²

а угловое ускорение

ε = a/R

тогда

0,5m₃R² · a/R = T₂R - T₁R

или

0,5m₃a = T₂ - T₁               (3)

Выразим  T₁  и  T₂ из уравнений (1) и (2)

T₁ = m₁a + m₁gμ           (4)

T₂ = m₂g - m₂a              (5)

и подставим полученные выражения в уравнение (3)

0,5m₃a = m₂g - m₂a  - (m₁a + m₁gμ)

откуда ускорение системы

Силы натяжения нити из выражений (4) и (5)

T₁ = 0,5 · 5,232 + 0,5 · 9,81 · 0,2 = 3,597 (Н) ≈ 3,6 Н.

T₂ =0,9 · 9,81 - 0,9 · 5,232 = 4,1202 (Н) ≈ 4,1 Н.