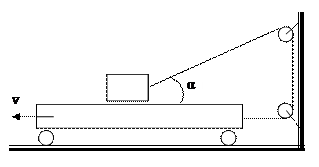
Небольшой брусок через систему блоков связан с тележкой нерастяжимой нитью. Тележку приводят в движение с постоянной скоростью v equals 4 space м divided by с. Какую скорость относительно тележки будет иметь брусок в тот момент, когда угол между наклонной нитью и горизонтом составит alpha equals 37 degree. Ответ выразить в м/с, округлить до десятых.
Приложения:
Ответы на вопрос
Ответил IUV
0
х - координата тележки
у - координата груза
h - разность высот блоков
L - длина нити
L=x+ h+корень(h^2+y^2)
x=v*t
y = корень((L-x-h)^2-h^2) =корень((L-v*t-h)^2-h^2)
y` =1/2*1/корень((L-v*t-h)^2-h^2) * 2*(L-v*t-h)*(-v) =1/y *(L-v*t-h)*(-v)
(x-y)`=v+1/y *(L-v*t-h)*v=v+1/y *(L-x-h)*v=v*(1+корень(h^2+y^2)/y) =
=v*(1+1/cos(alpha)) =4*(1+1/cos(37)) м/с = 9,00854263 м/с ~ 9,0 м/с
у - координата груза
h - разность высот блоков
L - длина нити
L=x+ h+корень(h^2+y^2)
x=v*t
y = корень((L-x-h)^2-h^2) =корень((L-v*t-h)^2-h^2)
y` =1/2*1/корень((L-v*t-h)^2-h^2) * 2*(L-v*t-h)*(-v) =1/y *(L-v*t-h)*(-v)
(x-y)`=v+1/y *(L-v*t-h)*v=v+1/y *(L-x-h)*v=v*(1+корень(h^2+y^2)/y) =
=v*(1+1/cos(alpha)) =4*(1+1/cos(37)) м/с = 9,00854263 м/с ~ 9,0 м/с
Ответил Аноним
0
Спасибо:*
Ответил IUV
0
на здоровье
Новые вопросы
Алгебра,
2 года назад
Английский язык,
2 года назад
Алгебра,
9 лет назад
Математика,
9 лет назад
Математика,
9 лет назад