Математика, вопрос задал Аноним , 1 год назад

не пишите бред пожалуйста это очень срочно

Приложения:

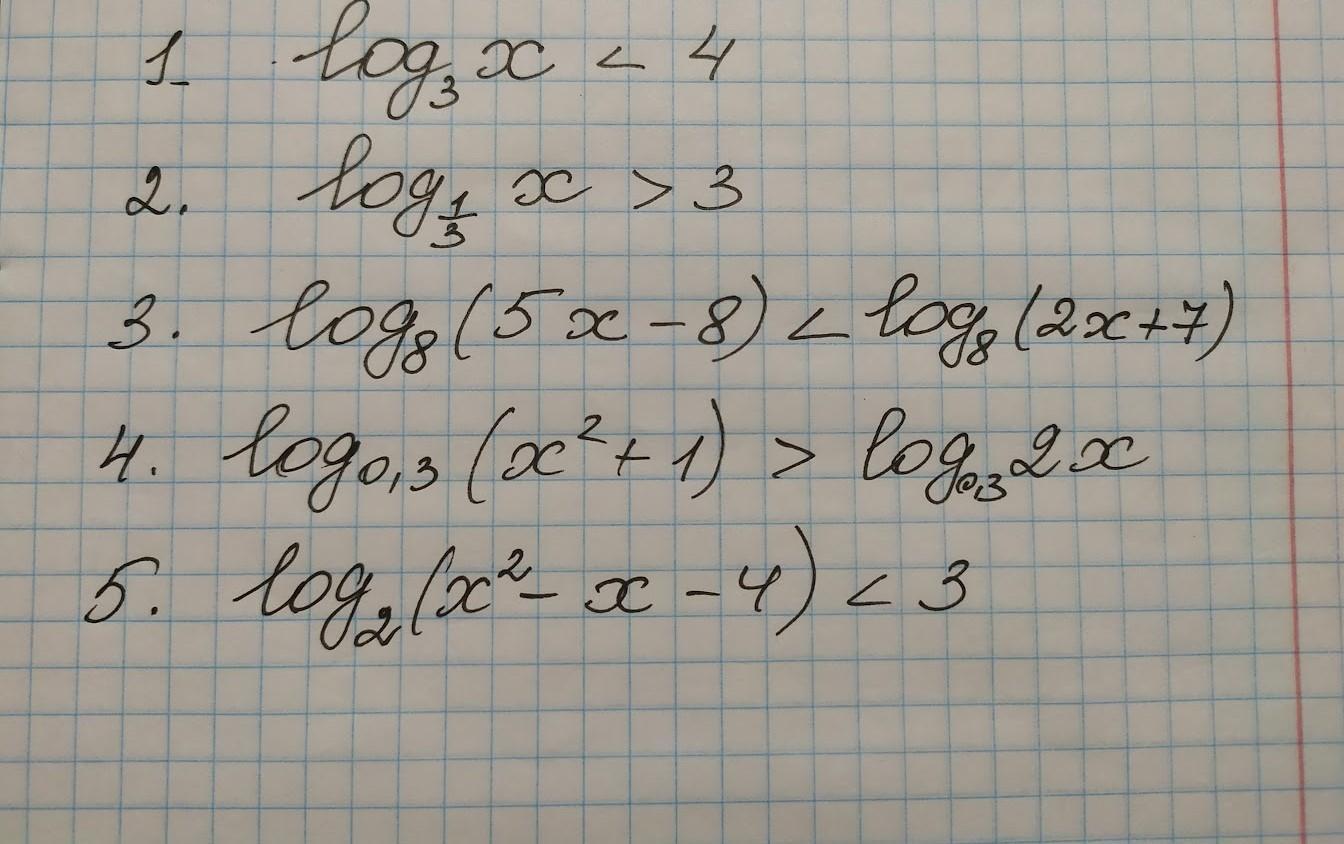
Ответы на вопрос

Ответил Аноним

0

1.

$\log_3{x} < 4\\x < 3^4\\x < 81$

2.

$\log_{\frac{1}{3}}x > 3\\x > \frac{1}{3}^3\\\\x > \frac{1}{27}$

3.

$\log_8(5x-8) < \log_8(2x+7)\\\log_8(5x-8)-\log_8(2x+7) < 0\\\log_8{\frac{5x-8}{2x+7}} < 0\\\frac{5x-8}{2x+7} < 1\\5x-8 < 2x+7\\3x < 15\\x < 5$

4.

$\log_{0.3}(x^2+1) > log_{0.3}{2x}\\\log_{0.3}(x^2+1)-log_{0.3}2x > 0\\\log_{0.3}(\frac{x^2+1}{2x}) > 0\\\frac{x^2+1}{2x} > 1\\x^2+1 > 2x\\x^2-2x+1 > 0\\x = \frac{2+\sqrt{4-4}}{2} = 1\\x > 1$

5.

$\log_2(x^2-x-4) < 3\\x^2-x-4 < 8\\x^2-x-12 < 0\\x1 = \frac{1+\sqrt{1+48}}{2} = \frac{1+7}{2} = 4\\x2 = \frac{1-\sqrt{1+48}}{2} = \frac{1-7}{2} = -3\\$

Нанесем корни на числовую ось и определим промежутки, на которых выражение < 0 (см. рисунок).

Выражение отрицательно на промежутке от -3 до 4.

Ответ: $-3 < x < 4$

Приложения:

Предыдущий вопрос

Следующий вопрос

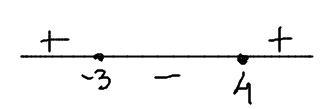
Новые вопросы

Физика, 1 год назад

Опір нагрівального елемента електропечі становить 25 Ом, а сила струму в ньому дорівнює 4 А. Скільки теплоти виділиться в цій електропечі за 5 хвилин?

Английский язык, 1 год назад

My favorite film 4 речень гари потер...

Русский язык, 1 год назад

ДАМ 25 баллов 1.На палубе п…рохода ра…пол…жились камен…щики груз…ики п…чники. 2.Они ехали на новые стр…ительные об…екты. 3.Все любовались ос…нним п…йзаж…м ра…матривали окрес…ности. 4.В воздухе...

Математика, 1 год назад

Розкладіть на множники!!! 1) m(a − b) + n(a − b); 2) g(4a - 2b) - f(4a - 2b); 3) 4n(x + y) — 3m(x + y). 4)mx-my+nx-ny 5)7a+7b-xa+xb Допоможіть!!

Русский язык, 6 лет назад

сочинение Первый раз в музее ...

Математика, 6 лет назад

a)1.6×(-4.5) б)-135.2:(-6.5) в)-1 7/8×1 1/3 г)1 2/3: (-3 1/3)...