Алгебра, вопрос задал hasanyanovemir , 1 год назад

Не обчислюючи коренів x1 та x2 рівняння 3x^2 - 8X - 15 = 0 знайти(дивіться прикріплене фото)

Приложения:

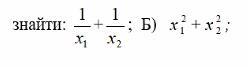
Ответы на вопрос

Ответил сок111213

По теореме Виета:

$a {x}^{2} + bx + c = 0\\ x_{1} + x_{2} = - \frac{b}{a} \\ x_{1} x_{2} = \frac{c}{a}$

$3 {x}^{2} - 8x - 15 = 0 \\ x_{1} + x_{2} = \frac{8}{3} \\ x_{1} x_{2} = - \frac{ 15}{3} = - 5 \\ \\ a) \: \frac{1}{x_{1}} + \frac{1}{x_{2}} = \frac{x_{1} + x_{2}}{x_{1}x_{2}} = \frac{8}{3} \div ( - 5) = - \frac{8}{15} \\ b) \: {x_{1}}^{2} + {x_{2}}^{2} = {x_{1}}^{2} + 2x_{1}x_{2} + {x_{2}}^{2} - 2x_{1}x_{2} = \\ = (x_{1} + x_{2}) {}^{2} - 2x_{1}x_{2} = ( \frac{8}{3} ) {}^{2} - 2 \times ( - 5) = \\ = \frac{64}{9} + 10 = 7 \frac{1}{9} + 10 = 17 \frac{1}{9}$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 11 месяцев назад

3.Амалдардың орындалу тәртiбiн аныкта және есепте. 57892:41*4+64400:280=...

География, 11 месяцев назад

Використовуючи дані з малюнка 2, визначте відносну висоту(у метрах) точок А,Б,В відносно дерева.

Математика, 1 год назад

СРОЧНОО Туристи мали пройти 90 км. До зупинки вони подолали 1/6 усього шляху, а після зупинки 4/5 шляху, який подолали до зупинки. Скільки всього кілометрів пройшли туристи?

Английский язык, 1 год назад

Даю 60 балов, срочно!!

География, 6 лет назад

РЕБЯТ ПОМОГИТЕ Я СПАТЬ ХОЧУ 6 КЛАСС...

Физика, 6 лет назад

Чому корпус автомобіля під час руху електризується, а корпус підводного човна - ні?