Математика, вопрос задал sanyka30122002 , 6 лет назад

Найти второй дифференциал.

Приложения:

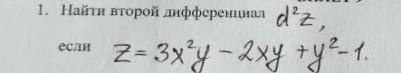
amanda2sempl: d²z/dx² = 6y, d²z/dy² = 2, d²z/(dxdy) = d(6xy - 2y)/dy = 6x - 2 ⇒
d²z = 6ydx² + 2(6x - 2)dxdy + 2dy²

Ответы на вопрос

Ответил pushpull

Ответ:

Пошаговое объяснение:

$\displaystyle z=3x^2y-2xy+y^2-1$

формула для второй производной функции двух переменных

$\displaystyle d^2z = z''_{xx}dx^2+2z''_{xy}dxdy+z''_{yy}dy^2$

найдем нужные частные производные

$\displaystyle z'_x=6xy-2y\qquad \qquadz''_{xx}= 6y\\\\z'_y = 3x^2-2x+2y\qquad z''_{yy}=2\\\\z''{xy}=6x-2$

и теперь ответ

$\displaystyle d^2z=6ydx^2+2(6x-2)dxdy+2dy^2$

Новые вопросы

Русский язык, 1 год назад

Русский язык, 1 год назад

Геометрия, 6 лет назад

Математика, 6 лет назад

Литература, 8 лет назад

Алгебра, 8 лет назад