найти точки экстремума функции y=2x ^3-3x^2
Ответы на вопрос
Ответил Аноним
0
1. Определяем область определения функции
D(y) = R
2. Вычислим производную

3. Производная равна 0

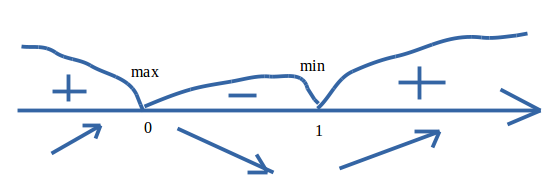
4. На промежутке смотреть во вложения.
Ответ:
 .
.
D(y) = R
2. Вычислим производную
3. Производная равна 0
4. На промежутке смотреть во вложения.
Ответ:
Приложения:
Новые вопросы