Найти точки экстремума функции:

найдем производную y'=6x²-18x+12 и найдем, при каких значениях х у'=0 (точки экстремума)
6x²-18x+12=0⇒x²-3x+2=0⇒x₁=2  x₂=1
найдем вторую производную
y''=12x-18
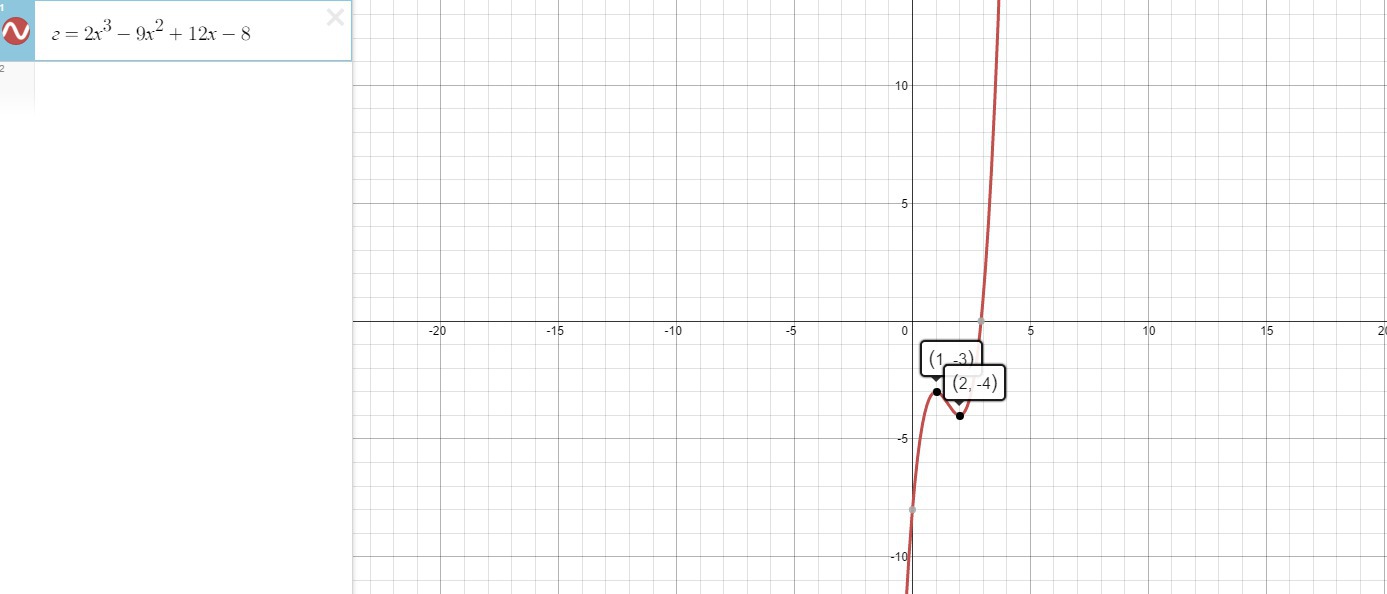
y''(1)=12-18=-6<0, в точке х=1 функция имеет максимум y(1)=2-9+12-8=-3
y''(2)=24-18=6>0, в точке х=2 функция имеет минимум у(2)=16-36+24-8=-4