Найти промежутки убывания/экстремумы/уравнение касательной к функции.
Приложения:
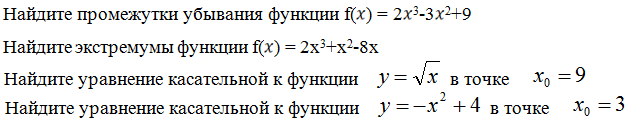
Ответы на вопрос
Ответил Аноним
0
__+___|____-___|____+__
0 1
Убывает на промежутке (0;1)
Уравнение касательной
y' = (-x²+4)' = -2x
следовательно:
f'(3) = -2 3 = -6
В результате имеем:
f(x) = y0 + y'(x0)(x - x0)
f(x) = 13-6x
Ответил Аноним
0
1)y`=6x²-6x=6x(x-1)=0
x=0 x=1
+ _ +
--------------------------------------------
возр 0 убыв 1 возр
max min
возр x∈(-∞;0) U (1;∞)
убыв x∈(0;1)
2)y`=6x²+2x-8=2(3x²+x-4)=0
D=1+24=25
x1=(-1-5)/6=-1 U x2=(-1+5)/6=2/3
+ _ +
--------------------------------------------
возр -1 убыв 2/3 возр
max min
y(-1)=-2+1+8=7
y(2/3)=16/27+4/9-16/3=(16+12-144)/27=-116/27
3)y(9)=3
y`=1/2√x
y`(9)=1/6
Y=3+1/6(x-9)=3+1/6x-3/2=1/6x+3/2
4)y(3)=-9+4=-5
y`=-2x
y`(3)=-6
Y=-5-6(x-3)=-5-6x+18=-6x+13
x=0 x=1
+ _ +
--------------------------------------------
возр 0 убыв 1 возр
max min
возр x∈(-∞;0) U (1;∞)
убыв x∈(0;1)
2)y`=6x²+2x-8=2(3x²+x-4)=0
D=1+24=25
x1=(-1-5)/6=-1 U x2=(-1+5)/6=2/3
+ _ +
--------------------------------------------
возр -1 убыв 2/3 возр
max min
y(-1)=-2+1+8=7
y(2/3)=16/27+4/9-16/3=(16+12-144)/27=-116/27
3)y(9)=3
y`=1/2√x
y`(9)=1/6
Y=3+1/6(x-9)=3+1/6x-3/2=1/6x+3/2
4)y(3)=-9+4=-5
y`=-2x
y`(3)=-6
Y=-5-6(x-3)=-5-6x+18=-6x+13
Новые вопросы
Химия,
1 год назад
Математика,
1 год назад
Геометрия,
1 год назад
Математика,
1 год назад
Математика,
7 лет назад