Найти производные, пожалуйста! на фото
Приложения:
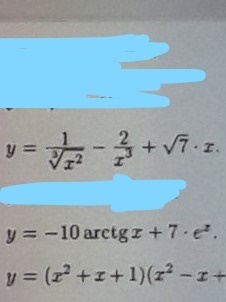
Ответы на вопрос
Ответил paradiseva
0
==============================
Новые вопросы
Українська література,
2 года назад
Математика,
7 лет назад
Математика,
7 лет назад
Литература,
8 лет назад
Математика,
8 лет назад