Алгебра, вопрос задал dori4ak , 6 лет назад

найти производную, с подробным решением, как надо! пример на фото.

Приложения:

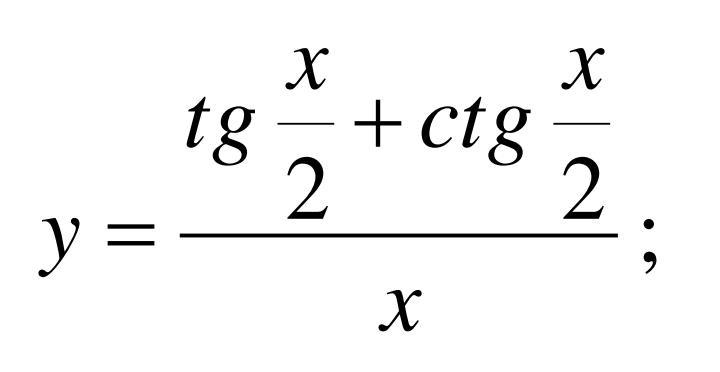
Ответы на вопрос

Ответил sangers1959

Объяснение:

$y=\frac{tg\frac{x}{2}+ctg\frac{x}{2} }{x}=\frac{\frac{sin\frac{x}{2} }{cos\frac{x}{2} } +\frac{cos\frac{x}{2} }{sin\frac{x}{2} } }{x}=\frac{\frac{sin^2\frac{x}{2}+cos^2\frac{x}{2} }{sin\frac{x}{2}*cos\frac{x}{2} } }{x}=\frac{\frac{1}{sin\frac{x}{2}*cos\frac{x}{2} } }{x}=\frac{1}{x*sin\frac{x}{2}*cos\frac{x}{2} } =\\=\frac{1*2}{x*2*sin\frac{x}{2}*cos\frac{x}{2} } =\frac{2}{x*sinx}. \\$

$y'=(\frac{2}{x*sinx})'=(\frac{2x^{-1}}{sinx})'=\frac{(2x^{-1})'*sinx-2x^{-1}*(sinx)'}{sin^2x} =\frac{-2*x^{-2}*sinx-2x^{-1}*cosx}{sin^2x}=\\=\frac{-2x^{-2}*(sinx+x*cosx)}{sin^2x} =-\frac{2*(sinx+x*cosx)}{x^2*sin^2x} .$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Будут ли проверочными к слову помирились слова: мерить, мирить?

Английский язык, 1 год назад

Перевод! 1)-Хелен,подойди сюда! Сколько тебе лет? -Пять.У тебя есть любимчик?-Да у меня есть собака.-Это он или она? Это он.-Как его зовут?-Его зовут Бим.-А сколько ему лет?-ему 7 месяцев ,но он...

Русский язык, 6 лет назад

Разбери слова по составу. В скобках укажи, какими частями речи они являются. общежитие, присмотрелся, лисичка, приморский, секретный, приготовим.

География, 6 лет назад

5. Обведите правильный ответ. 1) река Норка от пристани до посёлка Лесков течёт на восток, 2) овраг расположен восточнее реки Быстрая 3) на правом берегу реки Норка находится пристань 4) посёлок...

Математика, 8 лет назад

9-6x=3x-6 решите пожалуйста...

Литература, 8 лет назад

Почему Герасим проявляет великодушие по отношению к Татьяне...