Алгебра, вопрос задал 25hjoerf10 , 6 лет назад

Найти производную функции.
Нужен ответ, как на 2-ом фото.

Приложения:

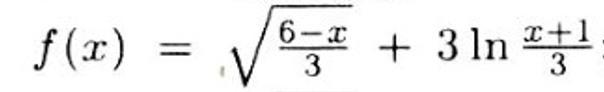
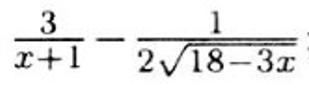
Ответы на вопрос

Ответил sangers1959
0

Ответ:

Объяснение:

f(x)=sqrt{frac{6-x}{3} }+3*lnfrac{x+1}{3} \f'(x)=(sqrt{frac{6-x}{3} }+3*lnfrac{x+1}{3})'=(sqrt{frac{6-x}{3} })'+(3*lnfrac{x+1}{3})'=\=((frac{6-x}{3} )^{frac{1}{2} })'+3*frac{1}{frac{x+1}{3} } *(frac{x+1}{3} )'=frac{1}{2} *(frac{6-x}{3})^{-frac{1}{2} }*(frac{6-x}{3})'+frac{3*3}{3*(x+1)} =\ =-frac{1}{6}*sqrt{frac{3}{6-x} } +frac{3}{x+1} =frac{3}{x+1}-frac{sqrt{3} }{6sqrt{6-x} } =frac{3}{x+1}- frac{1}{2sqrt{3} *sqrt{6-x} } =frac{3}{x+1}-frac{1}{2sqrt{18-3x} } .

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Математика, 1 год назад
0,02x + 0,5x + 0,092 = 0,3...
Русский язык, 1 год назад
Придумайте пожалуйста небольшой рассказ и употребить в нем любую поговорку...
Математика, 6 лет назад
ОЧЕНЬ СРОЧНО !!!!!!!!!
Математика, 6 лет назад
Заполните таблицу (10 баллов)...
Математика, 8 лет назад
СРОЧНО НУЖНО (5 в квадрате-4 в квадрате)в кубе=(25-16)в кубе=9в кубе...
Математика, 8 лет назад
В задача было сказано: Тренеровка Алисы начинается в 18часов, а заканчивается в 19часов 30 минут. Сколько времени длится тренеровка? Выразите это время а) в часах и минутах, б) в минутах. какое...