Математика, вопрос задал Аноним , 2 года назад

Найти производную функции и значение производной в точке X0

Приложения:

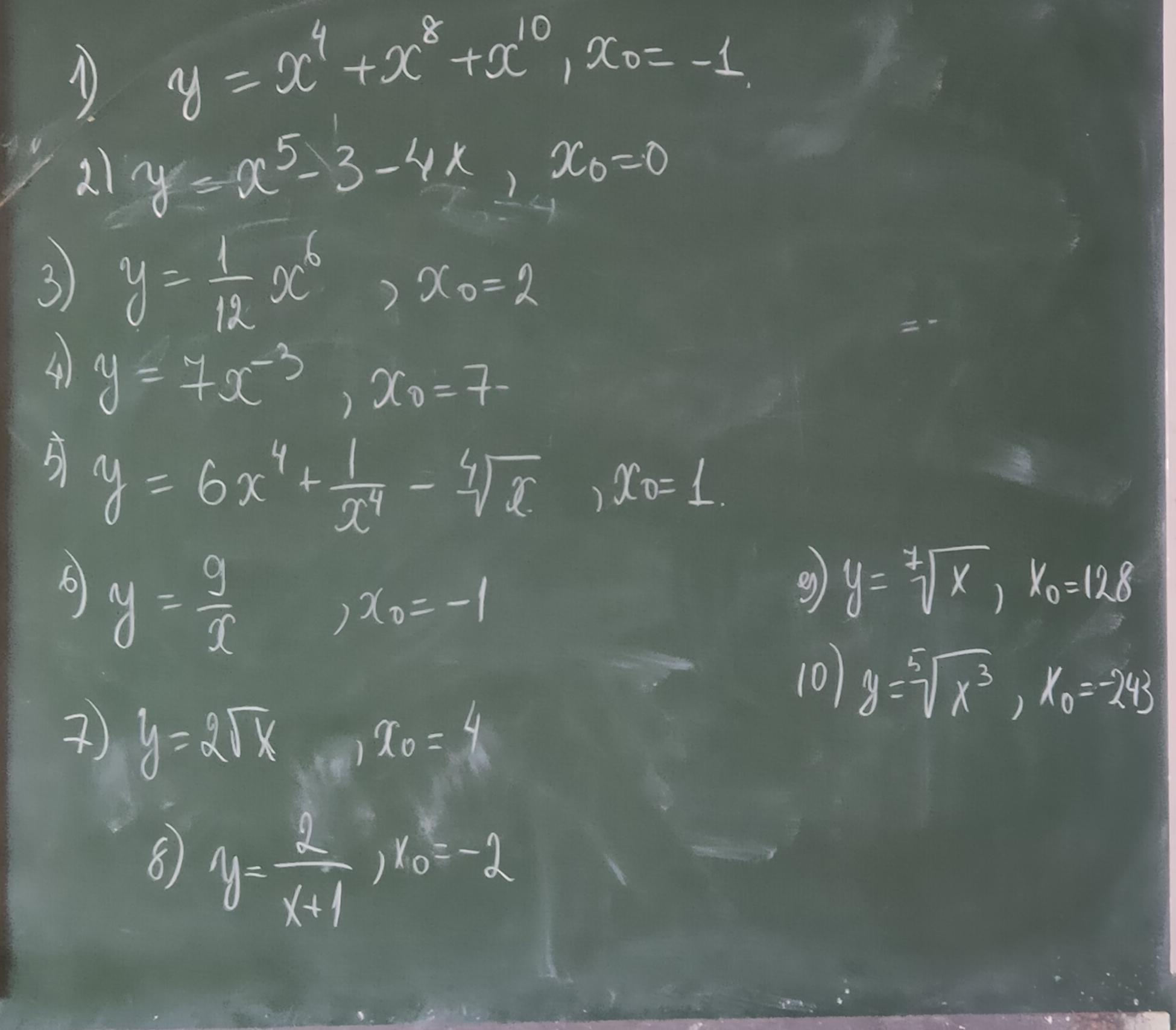
Ответы на вопрос

Ответил Miroslava227

Ответ:

$y '= 4 {x}^{3} + 8 {x}^{7} + 10 {x}^{9} \\ y'( - 1) = - 4 - 8 - 10 = - 22$

$y' = 5 {x}^{4} - 4 \\ y'(0) = - 4$

$y' = \frac{1}{2} {x}^{5} \\ y'(2) = {2}^{4} = 16$

$y' = - 21 {x}^{ - 4} = - \frac{21}{ {x}^{4} } \\ y'(7) = - \frac{21}{7 \times {7}^{3} } = - \frac{3}{343}$

$y' = 24 {x}^{3} - 4 {x}^{ - 5} - \frac{1}{4} {x}^{ - \frac{3}{4} } = \\ = 24 {x}^{3} - \frac{4}{ {x}^{5} } - \frac{1}{4 \sqrt[4]{ {x}^{3} } }$

$y'(1) = 24 - 4 - 0.25 = 20 - 0.25 = 19.75 \\$

$y' = - 9 {x}^{ - 2} = - \frac{9}{ {x}^{2} } \\ y'( - 1) = - 9$

$y '= 2 \times \frac{1}{2} {x}^{ - \frac{1}{2} } = \frac{1}{ \sqrt{x} } \\ y'(4) = \frac{1}{2} = 0.5$

$y' = - 2 {(x + 1)}^{ - 2} = - \frac{2}{ {(x + 1)}^{2} } \\ y'( - 2) = - \frac{2}{1} = - 2$

$y' = \frac{1}{7} {x}^{ - \frac{6}{7} } = \frac{1}{7 \sqrt[7]{ {x}^{6} } } \\ y'(128) = \frac{1}{ {7( \sqrt[7]{128} )}^{6} } = \frac{1}{7 \times {2}^{6} } = \\ = \frac{1}{7 \times 64} = \frac{1}{448}$

10.

$y' = \frac{3}{5} {x}^{ - \frac{2}{5} } = \frac{3}{5 \sqrt[5]{ {x}^{2} } } \\ y'( - 243) = \frac{3}{5 {( - 3)}^{2} } = \frac{1}{5 \times 3} = \frac{1}{15}$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Українська мова, 1 год назад

Казка про гриб скласти...

Қазақ тiлi, 1 год назад

СРОЧНО ( берілген есімшелерге көптік жалғауын жалғап,сөйлемдер қурандар. Айтқан,беретін,отырған,жазған,қаллырған.

Обществознание, 2 года назад

ПОМОГИТЕ ПРОШУ, УМОЛЯЮ!!! ПОЖАЛУЙСТА, ПОЖАЛУЙСТА, ПОЖАЛУЙСТА...

Қазақ тiлi, 2 года назад

Мәтін кейіпкерлерінің іс-әрекетіне қарап, берілген сипаттамалардың кімге тән екенін көрсетіңдер. АЛАДДИННИН МӘТІНІ ПЖ СРОЧНО ...

Литература, 7 лет назад

Созвездия посвящённая Орфею...

Математика, 7 лет назад

найдите число если 27% его равны 5400...