Математика, вопрос задал doekrin , 2 года назад

Найти производную dy/dx, если:

Приложения:

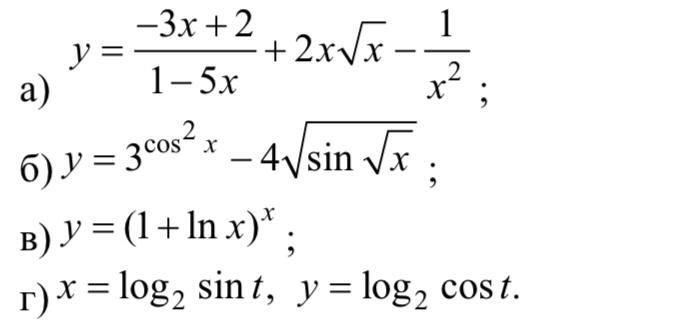
Ответы на вопрос

Ответил Miroslava227

2

Ответ:

а)

$y '= \frac{ - 3(1 - 5x) + 5(2 - 3x)}{ {(1 - 5x)}^{2} } + 2 \times \frac{3}{2} {x}^{ \frac{1}{2} } + 2 {x}^{ - 3} = \\ = \frac{ - 3 + 15x + 10 - 15x}{ {(1 - 5x)}^{2} } + 3 \sqrt{x} + \frac{2}{ {x}^{3} } = \\ = \frac{7}{ {(1 - 5x)}^{2} } + 3 \sqrt{x} + \frac{2}{ {x}^{3} }$

б)

$y' = ln(3) \times {3}^{ { \cos }^{2} (x)} \times 2 \cos(x) \times ( - \sin(x)) - 4 \times \frac{1}{2} {( \sin( \sqrt{x)} ) }^{ - \frac{1}{2} } \times \cos( \sqrt{x} ) \times \frac{1}{2 \sqrt{x} } = \\ = - ln(2) \sin(2x) \times {3}^{ { \cos}^{2} (x)} - \frac{ \cos( \sqrt{x} ) }{ 2 \sqrt{x} \sqrt{\sin( \sqrt{x} ) } }$

в)

$y = {(1 + ln(x)) }^{x} \\$

по формуле:

$y' = ( ln(y))' \times y$

$( ln(y))' = ( ln( {(1 + ln(x)) }^{x} )' = \\ = (x \times (ln( ln(x) + 1) )) '= \\ = ln( ln(x) + 1) + \frac{1}{ ln(x) + 1 } \times \frac{1}{x} \times x = \\ = ln( ln(x) + 1) + \frac{1}{ ln(x) + 1 }$

$y' = {(1 + ln(x)) }^{x} \times ( ln( ln(x) + 1) + \frac{1}{ ln(x) + 1} ) \\$

г)

$x = log_{2}( \sin(t) ) \\ y = log_{2}( \cos(t) )$

$y'x = \frac{y't}{x't} \\$

$y't = \frac{1}{ ln(2) \times \cos(t) } \times ( - \sin(t)) \\$

$x't = \frac{1}{ ln(2) \times \sin(t) } \times \cos(t) \\$

$y' x = - \frac{ \sin(t) }{ ln(2) \cos(t) } \times \frac{ ln(2) \sin(t) }{ \cos(t) } = \\ = - {tg}^{2} (t)$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Однокоренные к слову сверхискусный...

Русский язык, 1 год назад

Что за сказка из слог кахаржи...

Математика, 2 года назад

пластиковый горшок стал мутным после растворителя. Чем отмыть?

Биология, 2 года назад

Укажи, к каким системам органов относится каждый из органов. Семяпровод — . Рот — . Большие полушария переднего мозга — . Трахея — . Почки — .

Математика, 7 лет назад

Приведите обыкновенные дроби 1) 1/2 3/4 5/6 7/9 11/12 17/18 к обыкновенной дроби со знаминателем 36 2) 1/2 2/3 4/7 5/14 8/21 1/6 к обыкновенной дроби со знаминателем 42...

Литература, 7 лет назад

Речевая характеристика Скалозуба...