Найти предел функции при х стремящимся к Нулю
Приложения:
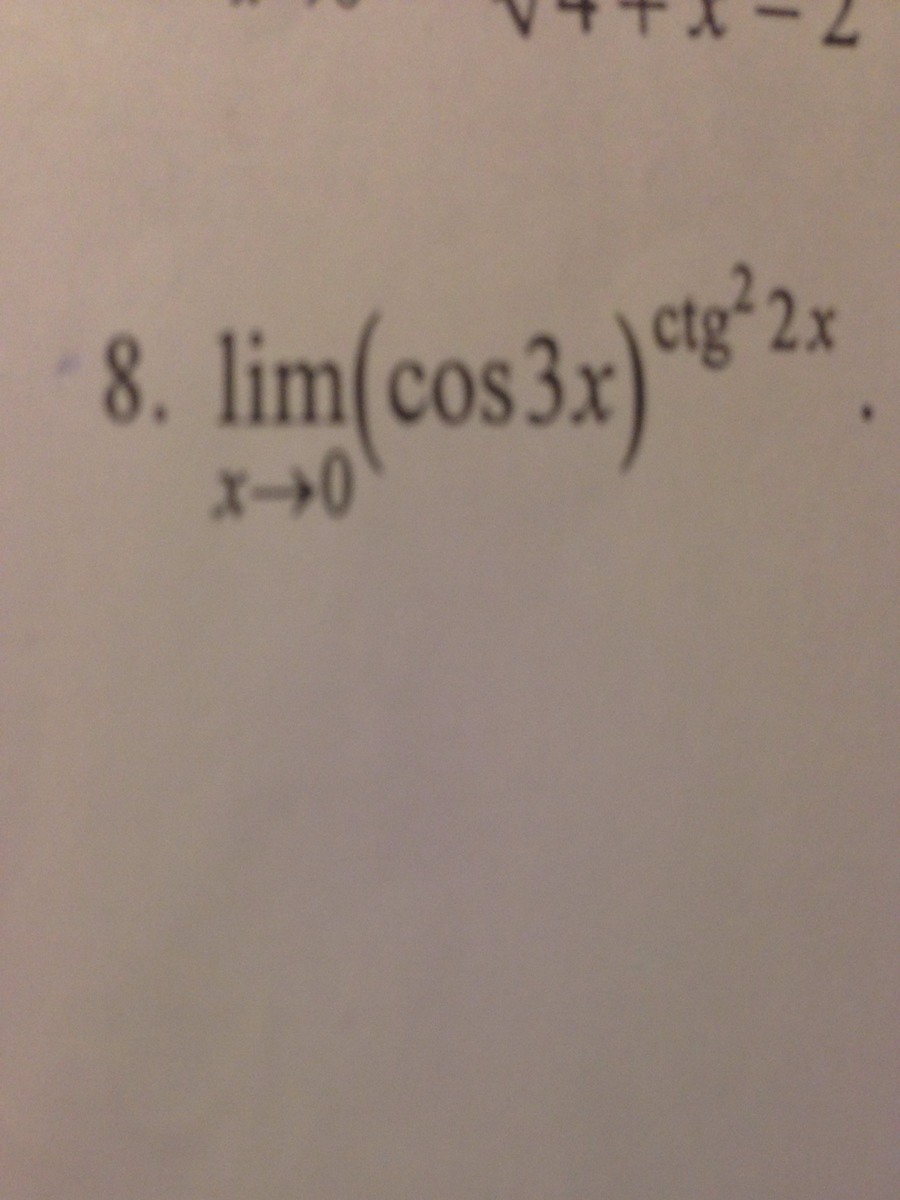
Ответы на вопрос
Ответил khadarak
0
lim cos3x ^ (ctg^2 2x)
мда, 1 в степени inf, тяжелый случай..
= lim cos3x^(cos^2 2x/sin^2 2x)
убиваем косинус в числителе показателя, в пределе он = 1
= lim cos3x^(1/sin^2 2x)
организуем второй замечательный предел
= lim (1+cos3x-1)^(1/sin^2 2x) =
= lim [(1+cos3x-1)^(1/cos 3x-1)]^((cos3x -1)/sin^2 2x) =
= exp [ lim (cos3x -1)/sin^2 2x)]
угу, e в степени 0/0, час от часу не легче
вспоминаем.. cos(a)-1 = 2 * sin^2 (a/2), меняем знак в числителе и выносим минус перед пределом
= exp [ -lim (1-cos3x)/sin^2 2x)] =
= exp [ -lim (sin^2(3/2 * x)/sin^2 2x)] =
походу, еще первый замечательный предел соорудить надо
= exp [ -lim (sin^2(3/2*x) * (2x) / sin^2(2x)* (3/2*x) * (3/2*x)/(2x)]
= exp [-lim (1/1 * 3/2* 1/2)] = exp (-3/4)
Ответ e^(-3/4)
мда, 1 в степени inf, тяжелый случай..
= lim cos3x^(cos^2 2x/sin^2 2x)
убиваем косинус в числителе показателя, в пределе он = 1
= lim cos3x^(1/sin^2 2x)
организуем второй замечательный предел
= lim (1+cos3x-1)^(1/sin^2 2x) =
= lim [(1+cos3x-1)^(1/cos 3x-1)]^((cos3x -1)/sin^2 2x) =
= exp [ lim (cos3x -1)/sin^2 2x)]
угу, e в степени 0/0, час от часу не легче
вспоминаем.. cos(a)-1 = 2 * sin^2 (a/2), меняем знак в числителе и выносим минус перед пределом
= exp [ -lim (1-cos3x)/sin^2 2x)] =
= exp [ -lim (sin^2(3/2 * x)/sin^2 2x)] =
походу, еще первый замечательный предел соорудить надо
= exp [ -lim (sin^2(3/2*x) * (2x) / sin^2(2x)* (3/2*x) * (3/2*x)/(2x)]
= exp [-lim (1/1 * 3/2* 1/2)] = exp (-3/4)
Ответ e^(-3/4)
Новые вопросы