Алгебра, вопрос задал 1Елеонора2 , 1 год назад

найти площадь треугольника который отсекает прямая 5х-3у-1=0 от координатного угла

Ответы на вопрос

Ответил NNNLLL54

Ответ:

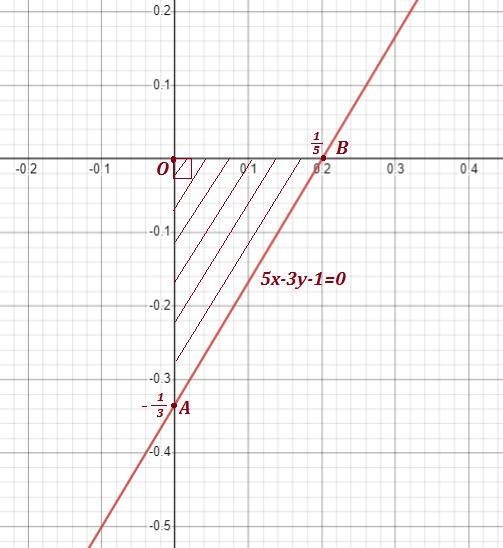
Прямая $\bf 5x-3y-1=0$ пересекает оси координат в точках

$\bf A(\ 0\ ;\ -\frac{1}{3}\ )$ и $\bf B(\ \frac{1}{5}\ ;\ 0\ )$ .

Эта прямая отсекает от координатного угла прямоугольный

треугольник АОВ , катеты которого равны 1/3 и 1/5 .

Площадь этого треугольника равна

$\bf S=\dfrac{1}{2}\cdot OA\cdot OB=\dfrac{1}{2}\cdot \dfrac{1}{3}\cdot \dfrac{1}{5}=\dfrac{1}{30}$ (ед²) .

Приложения:

Новые вопросы

Математика, 1 год назад

Математика, 1 год назад

Українська мова, 1 год назад

Алгебра, 1 год назад

Қазақ тiлi, 6 лет назад

Английский язык, 6 лет назад