Найти площадь фигуры y=-x^2-3x; y=0
Пожалуйста ;)
Ответы на вопрос
Ответил iiiiivvvv
0
Определим точки пересечения заданных линий:
x²+3x=0
x(x+3)=0
x=0
x=-3
Фигура, ограниченная этими линиями, заключена между отрезком (-3:0)-(0:0) и отрицательной частью параболы y=x²+3x.
Площадь фигуры есть абсолютное значение определенного интеграла от -3 до 0, примененный к функции x²+3x.
x²+3x=0
x(x+3)=0
x=0
x=-3
Фигура, ограниченная этими линиями, заключена между отрезком (-3:0)-(0:0) и отрицательной частью параболы y=x²+3x.
Площадь фигуры есть абсолютное значение определенного интеграла от -3 до 0, примененный к функции x²+3x.
Приложения:
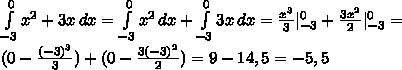
Ответил iiiiivvvv
0
Абсолютное значение равно 5,5.
Ответ: площадь фигуры равна 5,5.
Ответ: площадь фигуры равна 5,5.
Новые вопросы
Английский язык,
2 года назад
Математика,
8 лет назад
Обществознание,
8 лет назад
Математика,
9 лет назад