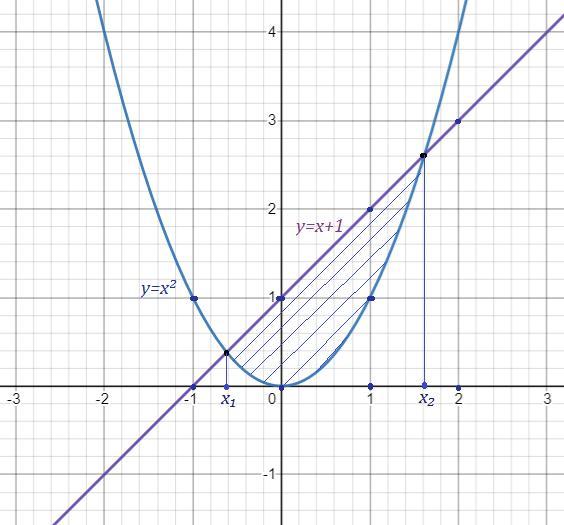
Алгебра, вопрос задал hxhdhwjwjjw , 6 лет назад

Найти площадь фигуры ограниченной параболой y=x^2 и прямой y=x+1.Помогите срочно с графиком

VоЛk: приравниваешь, находишь аналитически пределы интеграла. Находишь, какой график проходит выше. Интеграл от разницы высшего и низшего.

Ответы на вопрос

Ответил NNNLLL54

Ответ:

$y=x^2\ \ ,\ \ y=x+1\ ,\\\\x^2=x+1\ \ ,\ \ \ x^2-x-1=0\ \ ,\ \ D=1+4=5\ \ ,\\\\x_1=\dfrac{1-\sqrt5}{2}\approx -0,62\ \ ,\ \ x_2=\dfrac{1+\sqrt5}{2}\approx 1,62$

$S=\displaystyle \int\limits_{\frac{1-\sqrt5}{2}}^{\frac{1+\sqrt5}{2}}\, (x+1-x^2)\, dx=\Big(\frac{x^2}{2}+x-\frac{x^3}{3}\Big)\Big|_{\frac{1-\sqrt5}{2}}^{\frac{1+\sqrt5}{2}}=\\\\\\=\frac{(\frac{1+\sqrt5}{2})^2}{2}+\frac{1+\sqrt5}{2}-\frac{(\frac{1+\sqrt5}{2})^3}{3}-\frac{(\frac{1-\sqrt5}{2})^2}{2}-\frac{1-\sqrt5}{2}+\frac{(\frac{1-\sqrt5}{2})^3}{3}=\\\\\\=\frac{6+2\sqrt5}{8}+\frac{1+\sqrt5}{2}-\frac{16+8\sqrt5}{24}-\frac{6-2\sqrt5}{8}-\frac{1-\sqrt5}{2}+\frac{16-8\sqrt5}{24}=$

$\displaystyle =\frac{4\sqrt5}{8}+\frac{2\sqrt5}{2}+\frac{32}{24}=\frac{\sqrt5}{2}+\sqrt5+\frac{4}{3}=\frac{3\sqrt5+6\sqrt5+8}{6}=\frac{9\sqrt5+8}{6}\approx 4,69$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 1 год назад

в нескольких школьных буфетов завезли 750 пакетов кефира и молока.Каждая школа получила 25 пакетов кефира,а молока - в 5 раз больше , чем кефира.Во сколько школ завезли молоко и кефир?

Русский язык, 1 год назад

как обозначить звуками слово книга...

Информатика, 6 лет назад

Правильно определяет сколько осей у 3D- редактора помогите пожалуйста добрые люди ...

Математика, 6 лет назад

Решить уравнение Розв'язати рівняння 20баллов...

Математика, 8 лет назад

найди значение выражений 15+(12322:(24+37)-12*15):35*2-59...

Математика, 8 лет назад

Это уравнение по математике решите пожалуйста.