Найти площадь фигуры ограниченной линиями
y=-x^2+9 и y=0 (предварительно сделав рисунок).
juliaivanovafeo:
Какими линиями?
У обеих линий одно и то же уравнение?
да, написали так
В таком случае ответ - бесконечность
извенил
изменил, прости
Ответы на вопрос
Ответил juliaivanovafeo
1
Ответ:
36
Пошаговое объяснение:
Первый способ:Второй способ:
Так как график квадратичной функции симметричен относительно оси Oy, то площадь всей фигуры можно найти как удвоенную площадь одной из половин, например правой:
Приложения:
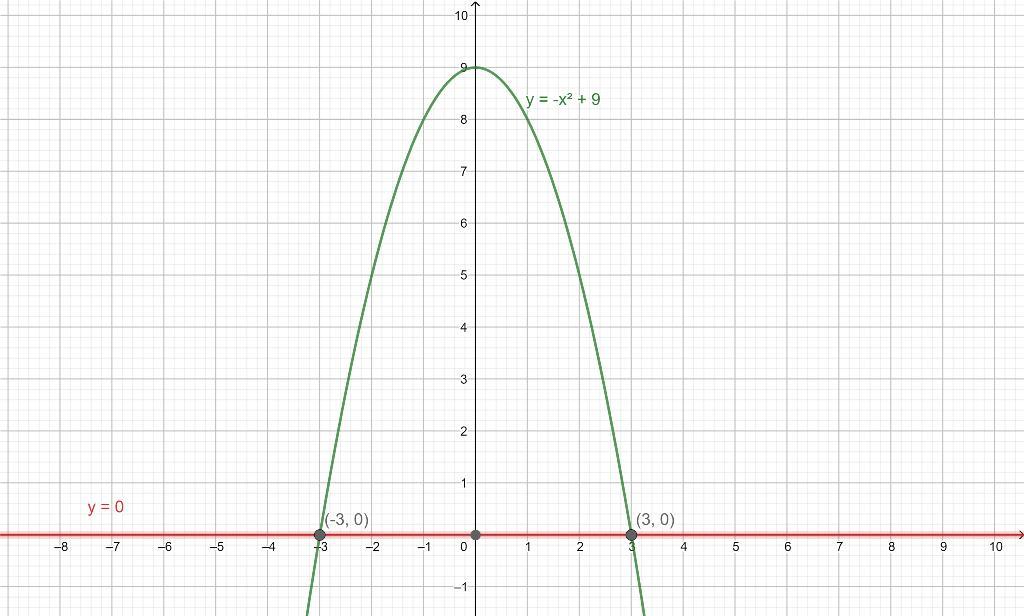
Спасибо большое
Новые вопросы
Другие предметы,
1 год назад
Английский язык,
1 год назад
Математика,
2 года назад
Алгебра,
7 лет назад