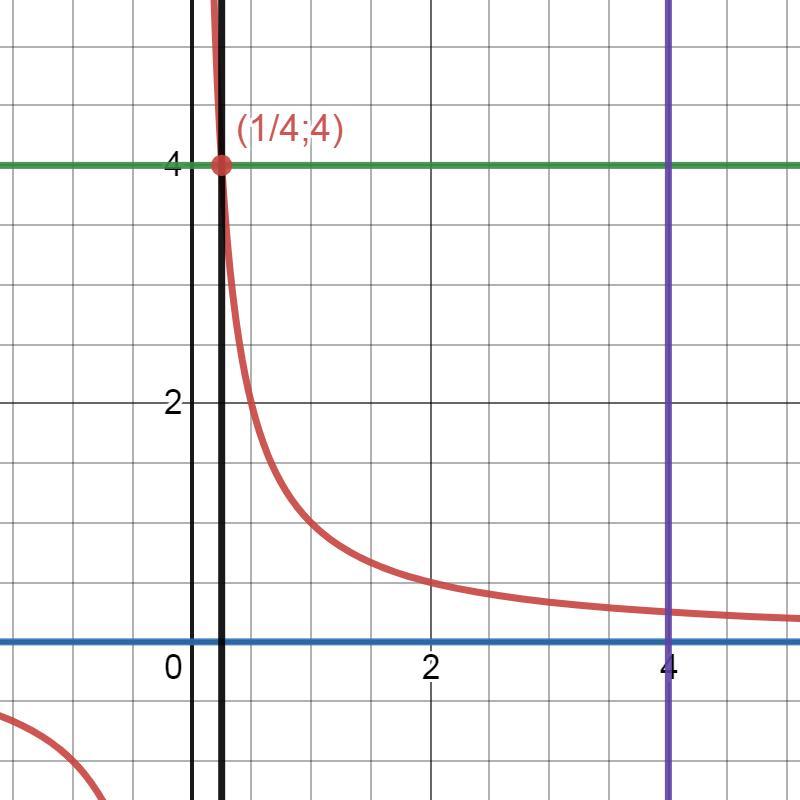
Математика, вопрос задал imadrid , 6 лет назад

Найти площадь фигуры, ограниченной линиями
y=1÷x , x=4 , y=4 , y=0

Ответы на вопрос

Ответил sangers1959

1

Пошаговое объяснение:

$y=\frac{1}{x} \ \ \ \ y=4\ \ \ \ \ x=4\ \ \ \ y=0\ \ \ \ S=?\\4=\frac{1}{x} \ \ \ \ \ x=\frac{1}{4}.\\ S=\int\limits^4_{\frac{1}{4}} {(4-\frac{1}{x}) } \, dx =(4x-ln|x|)\ |_{\frac{1}{4}}^4=4*4-ln4-(4*\frac{1}{4} -ln|\frac{1}{4}|)=\\ =16-ln4-1+ln4^{-1}=15-ln4-ln4=15-2*ln4=\\=15-ln4^2=15-ln16.$

Ответ: S≈12,2274 кв. ед.

Приложения:

imadrid: спасибо, помогите еще 2 примера на стене пожалуйста

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Напиши словосочетания в родительном падеже в единственном числе. Сильный ветер, хищный зверь, доброе дело, круглое бревно, острый карандаш, тонкое сукно, чайный прибор, холодный день. 2.Cпишите...

Русский язык, 1 год назад

распределите слова по группам. молоко,каникулы,нефть,сталь,чернила,прятки,шахматы,чистота,лень,сани,оттепель.

Английский язык, 6 лет назад

Допоможіть терміново!!!! Тільки 3 вправу...

Русский язык, 6 лет назад

отметь глаголы из каждой группы однокоренных слов. скрип, скрипеть, скрипучий, заскрипеть, подскрипывать. место,разместить,уместный,поместить,местность. серебро,серебрить, серебристый,посеребрить.

Обществознание, 8 лет назад

Верны ли следующие суждения об ограниченности ресурсов? А.Ограниченность ресурсов обусловлена ограниченностью потребностей человека. В. Общество стремится найти пути наилучшего использования...

Биология, 8 лет назад

что такое инстинкты и как они проявляются у членистоногих? Приведите примеры.