Математика, вопрос задал imadrid , 6 лет назад

Найти площадь фигуры, ограниченной линиями

Приложения:

Ответы на вопрос

Ответил sangers1959

Пошаговое объяснение:

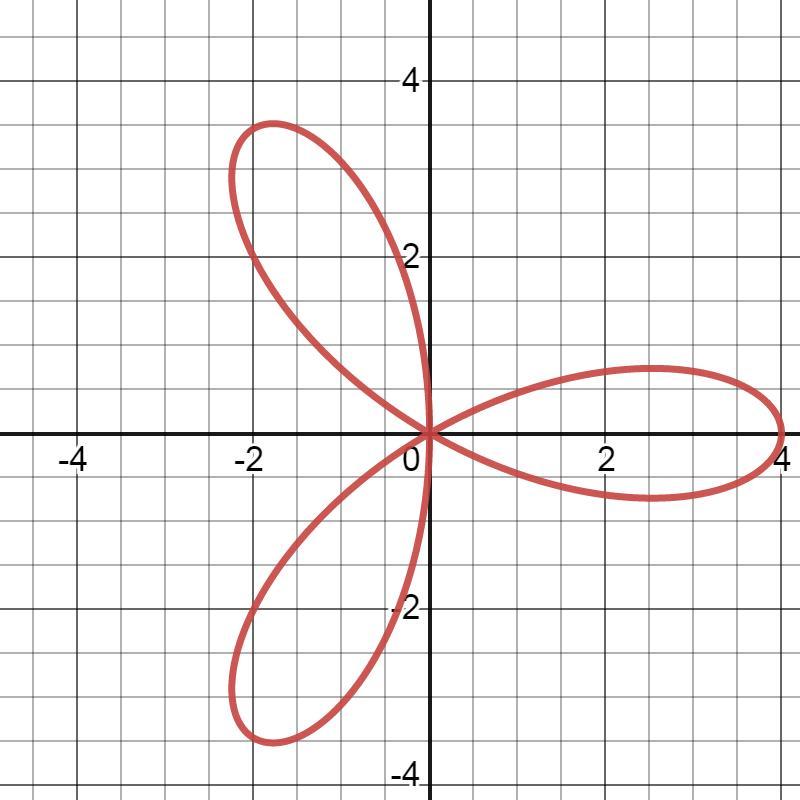
r=4*cos(3φ) r=2(r≥2) S=?

График лемнискаты Бернули см. ниже.

Найдём пределы интегрирования.

Данная кривая замкнута и симметрична относительно прямых:

r*cos(3φ)=0 и r*sin(3φ)=0. ⇒

r*cos(3φ)=0 |:r r*sin(3φ)=0 |:r

cos(3φ)=0. sin(3φ)=0.

3φ=π |:3 3φ=0 | :3

φ=π/3 φ=0.

Вычислим площадь одной лемнискаты:

$\int\limits^\frac{\pi }{3} _0 {r^2} \, d\phi =\int\limits^\frac{\pi }{3} _0 {(4^2*cos^2(3\phi))} \, d\phi =16*\int\limits^\frac{\pi }{3} _0 {(\frac{1+cos(2*3\phi}{2}) } \, d\phi =16*\frac{1}{2} *\int\limits^\frac{\pi }{3} _0 {(\frac{1+cos(6\phi)}{2}) } \, d\phi.\\\frac{1}{2}*\int\limits^{\frac{\pi }{3}} _0 {(1+cos(6\phi)) } \, d\phi= \frac{1}{2}*\int\limits^{\frac{\pi }{3}} _0d\phi+\frac{1}{2}*\int\limits^{\frac{\pi }{3}} _0cos(6\phi)d\phi=\\$

$=\frac{1}{2} *\phi\ |_0^{\frac{\pi }{3}} +\frac{1}{2}*\frac{1}{6} *sin(6\phi) |_0^{\frac{\pi }{3} }=\frac{\pi }{2*3} -\frac{1}{2}*0+\frac{sin\frac{6*\pi }{3} }{12} -\frac{sin(6*0)}{12}=\\=\frac{\pi }{6}-0+\frac{sin(2\pi ) }{12} -\frac{sin0}{12} =\frac{\pi }{6} -0+0-0=\frac{\pi }{6}.\ \ \ \ \ \ \ \Rightarrow\\16*\frac{\pi }{6} =\frac{8\pi }{3}.$

Так как у нас три лемнискаты, ⇒

$S=3*\frac{8\pi }{3}=8\pi .$

Ответ: S≈25,133 кв. ед.

Приложения:

imadrid: С помощью двойного интеграла вычислить площадь области D, ограниченной указанными линиями
1) D: y²=4x, x+y=3, y≥0

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Надо написать в негативной форме. Пожалуйста помогите. 1) We shall have returned here by the time you come. 2) I shall come back to you by next week. 3) My dress will have been ready by next Monday.

Українська мова, 1 год назад

Скласти речення з словосполученнями: пригощати борщем, мокнути під дощем, милуватися обличчям, відмикати двері ключем. Розказати хто б міг виконувати зазначені дії.