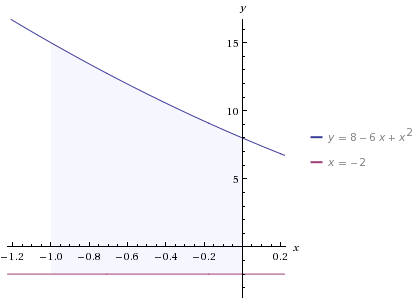
Алгебра, вопрос задал viktoriay974 , 9 лет назад

найти площадь фигуры ограниченной графиком f(x)=x^2-6x+8,прямыми x=-2,x=-1 и осью абсцисс

Ответы на вопрос

Ответил АннаАрт

$y=x^2-6x+8 \ x=-2 \ -1 leq x leq 0 \ \$

$intlimits^{0}_{-1} {(x^2-6x+10)} , dx = frac{x^3}{3} -6* frac{x^2}{2} +10x|^{0}_{-1}= frac{x^3}{3} -3x^2+10x|^{0}_{-1}= \ \ = (frac{0^3}{3} -3*0^2+10*0)-(frac{(-1)^3}{3} -3*(-1)^2+10*(-1))= \ \ =-(frac{-1}{3} -3*1+10*(-1))=-(frac{-1}{3} -3-10)= \ \ =-(frac{-1-3*3-10*3}{3})=-(frac{-1-9-30}{3})=-(frac{-40}{3})=frac{40}{3}=13,3333$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Химия, 2 года назад

Помогите пожалуйста Фонарик на щелочных элементах это источник света работающий от аккумуляторов на основе электролитов. Если у нас есть раствор гидроксида натрия с концентрацией 20 г/л и плотностью...

Алгебра, 2 года назад

Для функции f(x) = 3x 2 -5 найдите первообразную, график которой проходит через точку А(-1;3)...

Алгебра, 9 лет назад

y=x^3 cosx помогите решить...

Математика, 9 лет назад

После того как рабочий истратил 11% зарплаты у него осталось 33820р. Сколько всего составляет зарплата рабочего?

Математика, 9 лет назад

МАЛЬВИНА КУПИЛА 8 КОНФЕТ ПО a сольдо и b пирожных по 65 сольдо заплатив за конфеты меньше чем за пирожные. на сколько меньше заплатила МАЛЬВИНА за конфеты чем за пирожные? ВЫЧЕСЛИТЕ ЗНАЧЕНИЕ...

Математика, 9 лет назад

5 КЛАСС решите уравнения) 1)(39+х)-84=78,2)(600-х)-92=126,3)253-(х-459)=138,6)871-(х+157)=385 ...