Математика, вопрос задал gibihil , 2 года назад

Найти площадь фигуры, ограниченной графиками функций. Сделайте чертёж.

Приложения:

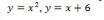
Ответы на вопрос

Ответил juliaivanovafeo

Ответ:

$20\frac{5}{6}$

Пошаговое объяснение:

$S = \int\limits^3_{-2} {(x + 6 - x^2)} \, dx = \\\\ = (\frac{x^2}{2} + 6x - \frac{x^3}{3} ) | ^3_{-2} = (\frac{3^2}{2} + 6 \cdot 3 - \frac{3^3}{3} ) - (\frac{(-2)^2}{2} + 6 \cdot (-2) - \frac{(-2)^3}{3} ) = \\\\ = (4,5 + 18 - 9) - (2 - 12 + \frac{8}{3} ) = 13,5 - (-7\frac{1}{3} ) = 13,5 + 7\frac{1}{3} = 20\frac{5}{6}$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Read and say yes or no. the toy soldier has got big green eyes...

Українська література, 1 год назад

як пишеться спілкування з друзями?

Алгебра, 2 года назад

Найдите точку пересечения графиков линейных функций y=3x-2 и y = - 2x+3 ( графически и алгебраический)...

Математика, 2 года назад

Сумма Трёх чисел 318 первое слагаемое наименьшее значное число первое наименьшее трёх значное число чему равно третье слагаемое...

Математика, 7 лет назад

Первая машинистка печатает 10 страниц в час, а вторая за 5 ч печатает столько же страниц, сколько первая за 4 ч. Сколько страниц отпечатают обе машинистки за 6 ч совместной работы?

Математика, 7 лет назад

Краткая запись!!!! Номер 15...