Найти общее решение дифференциального уравнения и частное решение удовлетворяющее начальному условию.
Приложения:
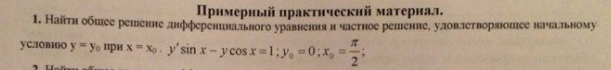
Ответы на вопрос
Ответил Vasily1975
0
Уравнение приводится к виду y'-y*ctg(x)=1/sin(x).
Пусть y=u*v, тогда уравнение примет вид u'*v+u*v'-u*v*ctg(x)-1/sin(x)=0,
v(u'-u*ctg(x))+u*v'-1/sin(x)=0. Приравнивая 0 выражение в скобках, получим уравнение u'=u*ctg(x) или du/u=ctg(x)*dx=cos(x)*dx/sin(x)=d(sin(x))/sin(x),
откуда ln(u)=ln(sin(x)), т.е. u=sin(x). Подставив найденное u в уравнение u*v'=1/sin(x), получим уравнение dv=dx/(sin(x)*sin(x))=-d(ctg(x)), откуда v=-ctg(x)+C. Тогда y=u*v=sin(x)*(-ctg(x)+C)= -cos(x)+C*sin(x)- общее решение. Используя начальное условие, получим уравнение 0 =0+С*sin(pi/2), или 0=0+ C, откуда С=0. Тогда частное решение y=-cos(x)
Пусть y=u*v, тогда уравнение примет вид u'*v+u*v'-u*v*ctg(x)-1/sin(x)=0,
v(u'-u*ctg(x))+u*v'-1/sin(x)=0. Приравнивая 0 выражение в скобках, получим уравнение u'=u*ctg(x) или du/u=ctg(x)*dx=cos(x)*dx/sin(x)=d(sin(x))/sin(x),
откуда ln(u)=ln(sin(x)), т.е. u=sin(x). Подставив найденное u в уравнение u*v'=1/sin(x), получим уравнение dv=dx/(sin(x)*sin(x))=-d(ctg(x)), откуда v=-ctg(x)+C. Тогда y=u*v=sin(x)*(-ctg(x)+C)= -cos(x)+C*sin(x)- общее решение. Используя начальное условие, получим уравнение 0 =0+С*sin(pi/2), или 0=0+ C, откуда С=0. Тогда частное решение y=-cos(x)
Новые вопросы