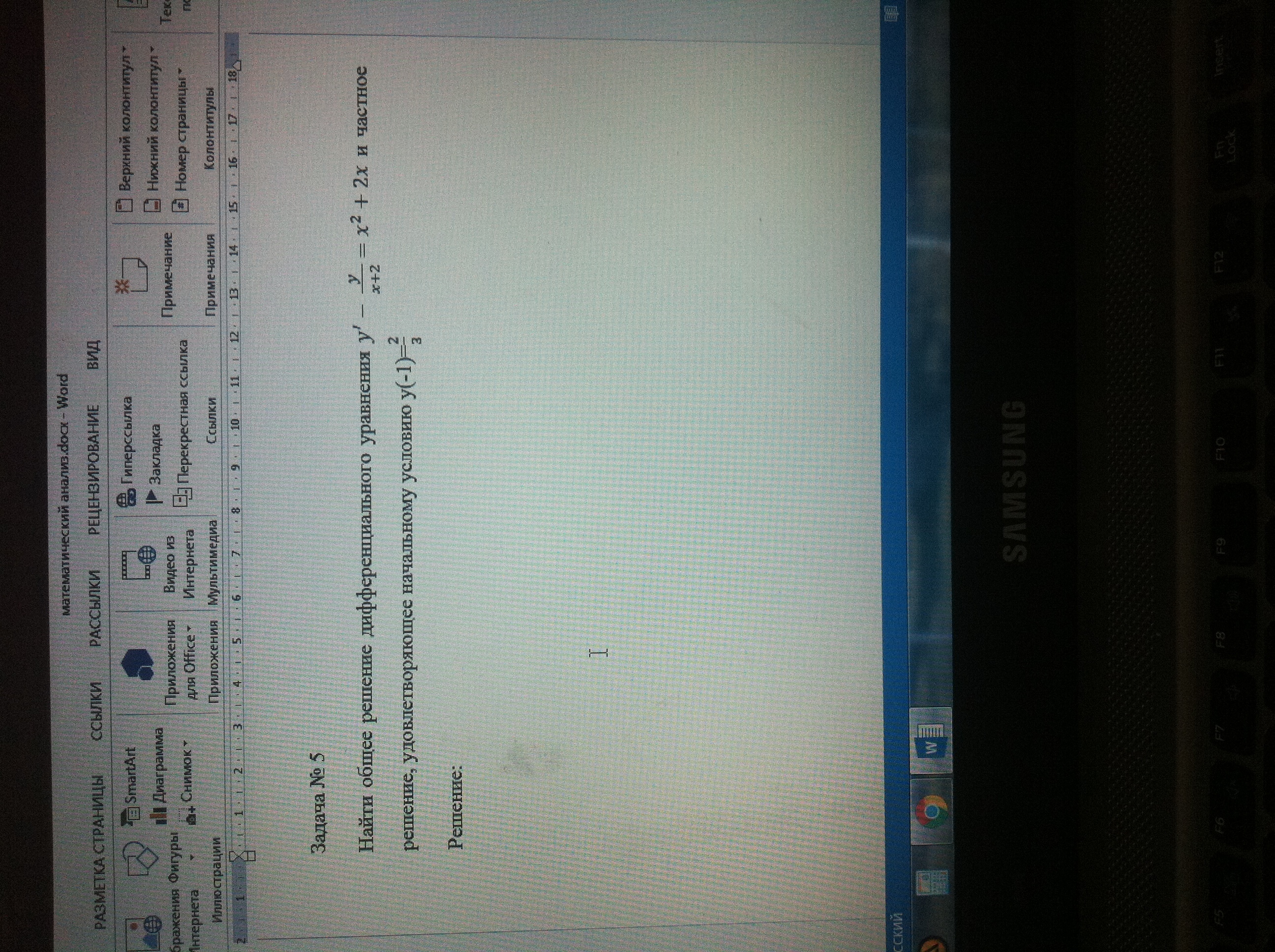
Математика, вопрос задал Katerino4ka90 , 8 лет назад

найти общее решение дифференциального уравнения...

Приложения:

Ответы на вопрос

Ответил Alexаndr

Это же легко... Неоднородный диффур
$y'-frac{y}{x+2}=x^2+2x\y=uv;y'=u'v+v'u\u'v+v'u-frac{uv}{x+2}=x^2+2x\u'v+u(v'-frac{v}{x+2})=x^2+2x\begin{cases}v'-frac{v}{x+2}=0\u'v=x^2+2xend{cases}\v'-frac{v}{x+2}=0\frac{dv}{dx}=frac{v}{x+2}|*frac{dx}{v}\frac{dv}{v}=frac{dx}{x+2}\intfrac{dv}{v}=intfrac{dx}{x+2}\ln|v|=ln|x+2|\v=x+2\u'(x+2)=x^2+2x|:x+2\frac{du}{dx}=x|*dx\du=xdx\int du=int xdx\u=frac{x^2}{2}+C\y=(x+2)(frac{x^2}{2}+C)=frac{x^3}{2}+x^2+C(x+2)\frac{2}{3}=-frac{1}{2}+1+C\C=frac{1}{6}$
$y=frac{x^3}{2}+x^2+frac{1}{6}(x+2)$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Алгебра, 2 года назад

1 , 2 , 3 пожалуйста...

Русский язык, 2 года назад

текст 1 _____________ Все, разумеется, помнят жестокую бурю, разразившуюся в этом году во время равноденствия. Барометр упал до 710 миллиметров. Страшный норд-ост дул, не утихая, с 18 по 26 марта. Он...

Информатика, 8 лет назад

Петя записал IP-адрес школьного сервера на листке бумаги и положил его в карман куртки. Петина мама случайно постирала куртку вместе с запиской. После стирки Петя обнаружил в кармане четыре обрывка с...

Литература, 8 лет назад

выдели слова писателя которые используешь в своём пересказе Пушкина "Сказка о мёртвой царевне"...

Математика, 9 лет назад

75 : 5 = 28 : 4 = 39 : 3 = 18 : 6 = 588 : 6 = 378 : 9 = 672 : 7 = 504 : 8 = 4315 : 5 = 4820 : 6 = 9820 : 5 = 3936 : 3 =...

Математика, 9 лет назад

впиши в пустые клетки подходящие числа. последню модел построй самостоятельно...