Алгебра, вопрос задал supergirl81 , 1 год назад

Найти область значений функции, помогите пожалуйста даю много баллов!

Приложения:

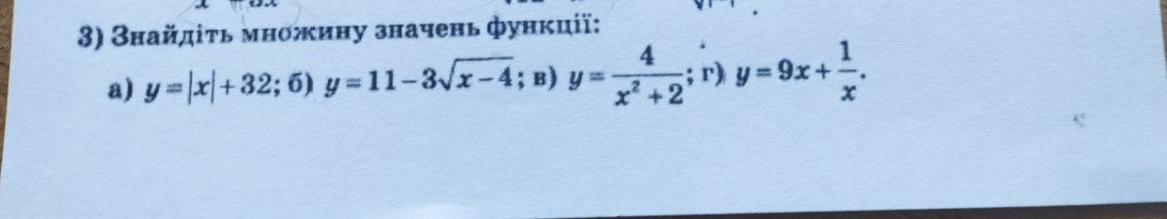
zau4ywka3004: Я конечно могу прислать своё решение, но гарантий что оно будет 100% правильным дать не могу

supergirl81: Буду благодарна коли решите)

supergirl81: *если

supergirl81: Присилайте

7x8: 1)
D(y)=R

|x|≥0 |+32
|x|+32≥32
Е(y)=[32;+∞)

7x8: Я не знаю, как ты это делал на уроке :(

Ответы на вопрос

Ответил 7x8

3

Ответ:

$1)\ E(y)=[32;+\infty)\\\\2)\ E(y)=(-\infty;11]\\\\3) E(y)=(0;2]\\\\4) E(y)=(-\infty;-6]\cup[6;+\infty)$

Объяснение:

1)

$y=|x|+32$

$D(y)=R$

$|x| \ge 0\ \ \ |+32$

$|x|+32 \ge 32$

$E(y)=[32;+\infty)$

2)

$y=11-3\sqrt{x-4}$

$D(y)=[4;+\infty)$

$\sqrt{x-4} \ge 0\ \ \ |\cdot 3$

$3\sqrt{x-4} \ge 0\ \ \ |\cdot(-1)$

$-3\sqrt{x-4} \le 0\ \ \ |+11$

$11-3\sqrt{x-4} \le 11$

$E(y)=(-\infty;11]$

Oбласть значений функции

Число $w$ принадлежит множеству значений функции $f$ тогда и только тогда, когда существует число $x$ такое, что $f(x) =w$ .

Значит нам нужно найти те значения $w$ , при которых уравнение $f(x)=w$ имеет хотя бы одно решение.

3)

$y=\frac{4}{x^2+2}$

$D(y)=R$

$\frac{4}{x^2+2}=w\ \ \ |\cdot(x^2+2)$

$(x^2+2)w=4$

$(x^2+2)w=4$

$wx^2+2w-4=0$

*

$w=0$

$-4=0$

нет решения

**

$w \neq 0$

$D=0^2-4\cdot w(2w-4)=-4w(2w-4)$

$D \ge 0$

$-4w(2w-4) \ge 0$

$-8w(w-2) \ge 0\ \ \ \ |:(-8)$

$w(w-2) \le 0$

$w\in [0;2]$

$w\in (0;2]$

$E(y)=(0;2]$

4)

$y=9x+\frac{1}{x}$

$E(y)=(-\infty;0)\cup(0;+\infty)$

$9x+\frac{1}{x}=w\ \ \ |\cdot x$

$9x^2+1=wx$

$9x^2-wx+1=0$

$D=(-w)^2-4\cdot 9\cdot 1=w^2-36$

$w^2-36 \ge 0$

$(w-6)(w+6) \ge 0$

$w\in (-\infty;-6]\cup[6;+\infty)$

$E(y)=(-\infty;-6]\cup[6;+\infty)$

aarr04594: По 3) є спосіб простіше, аналогічно другому, без заміни на параметр w.

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Алгебра, 11 месяцев назад

Срочно Срочно Срочно Срочно Срочно...

Химия, 11 месяцев назад

9. Проаналізуйте кількісний склад формули Ca(NO3)2: А) 1 атом Ca, 1 атом N, 3 атоми O; Б) 1 атом C, 2 атоми N, 6 атомів Н; В) 2 атоми Ca, 3 атоми О, 2 атоми N; Г) 1 атом Ca, 2 атоми N, 6 атомів O...

Українська мова, 1 год назад

Їх потрібно розділити на дві колонки та визначити ,що є словосполученням, а що ні. + Визначте головне й залежне слово в словосполученнях. Брат і сестра,виразне читання,на березі,читати голосно,у...

Биология, 1 год назад

ПОМОГИТЕ ПЖ ДАМ 30 БАЛЛОВВВ ЭТОТ СРОЧНААА...

Английский язык, 6 лет назад

Решите пожалуйста! Даю 15 баллов!️...

Математика, 6 лет назад

Помогите 27,14-30,21-2,3=...